题目内容
【题目】已知定义在R上的函数y＝f(x)对于任意的x都满足f(x＋1)＝－f(x)，当－1≤x＜1时，f(x)＝x3，若函数g(x)＝f(x)－loga|x|至少有6个零点，则a的取值范围是( )
A. 
∪(5，＋∞) B. 
∪
C. 
∪(5，7) D. ∪[5，7)
【答案】A
【解析】由f(x＋1)＝－f(x)得f(x＋1)＝－f(x＋2)，
因此f(x)＝f(x＋2)，即函数f(x)是周期为2的周期函数．
函数g(x)＝f(x)－loga|x|至少有6个零点可转化成y＝f(x)与h(x)＝loga|x|两函数图象交点至少有6个，需对底数a进行分类讨论．若a＞1，则h(5)＝loga5＜1，即a＞5.
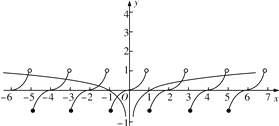
若0＜a＜1，则h(－5)＝loga5≥－1，即0＜a≤
.
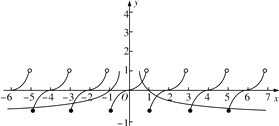
所以a的取值范围是
∪(5，＋∞)．故选A.
练习册系列答案
相关题目
【题目】网络购物已经被大多数人接受，随着时间的推移，网络购物的人越来越多，然而也有部分人对网络购物的质量和信誉产生怀疑。对此，某新闻媒体进行了调查，在所有参与调查的人中，持“支持”和“不支持”态度的人数如下表所示：
年龄 态度 | 支持 | 不支持 |
20岁以上50岁以下 | 800 | 200 |
50岁以 （含50岁） | 100 | 300 |
（1）在所有参与调查的人中，用分层抽样的方法抽取
个人，已知从持“支持”态度的人中抽取了9人，求
的值；
（2）是否有99.9%的把握认为支持网络购物与年龄有关？
参考数据：
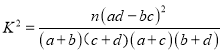，其中
，
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
