题目内容
【题目】已知f(x)=sin2(2x﹣ ![]() )﹣2tsin(2x﹣
)﹣2tsin(2x﹣ ![]() )+t2﹣6t+1(x∈[
)+t2﹣6t+1(x∈[ ![]() ,
, ![]() ])其最小值为g(t).
])其最小值为g(t).
(1)求g(t)的表达式;
(2)当﹣ ![]() ≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
≤t≤1时,要使关于t的方程g(t)=kt有一个实根,求实数k的取值范围.
【答案】
(1)解:∵x∈[ ![]() ,
, ![]() ],
],
∴sin(2x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
∴f(x)=[sin(2x﹣ ![]() ﹣t]2﹣6t+1,
﹣t]2﹣6t+1,
当t<﹣ ![]() 时,则当sinx=﹣
时,则当sinx=﹣ ![]() 时,f(x)min=
时,f(x)min= ![]() ;
;
当﹣ ![]() ≤t≤1时,当sinx=t时,f(x)min=﹣6t+1;
≤t≤1时,当sinx=t时,f(x)min=﹣6t+1;
当t>1时,当sinx=1时,f(x)min=t2﹣8t+2;
∴g(t)= 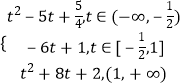
(2)解:当 ![]() 时,g(t)=﹣6t+1.令h(t)=g(t)﹣kt.
时,g(t)=﹣6t+1.令h(t)=g(t)﹣kt.
欲使g(t)=kt有一个实根,则只需使 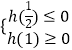 或
或 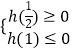 即可.
即可.
解得k≤﹣8或k≥﹣5.
【解析】(1)利用x的范围确定sin(2x﹣ ![]() ),对函数解析式化简整理,对t进行分类讨论,利用抛物线的性质求得每种情况的g(t)的解析式,最后综合.(2)根据(1)中获得当
),对函数解析式化简整理,对t进行分类讨论,利用抛物线的性质求得每种情况的g(t)的解析式,最后综合.(2)根据(1)中获得当 ![]() 时g(t)的解析式,令h(t)=g(t)﹣kt,要使g(t)=kt有一个实根需h(﹣
时g(t)的解析式,令h(t)=g(t)﹣kt,要使g(t)=kt有一个实根需h(﹣ ![]() )和h(1)异号即可.
)和h(1)异号即可.
【考点精析】关于本题考查的三角函数的最值,需要了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目