题目内容
【题目】某颜料公司生产![]() 两种产品,其中生产每吨
两种产品,其中生产每吨![]() 产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨
产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨![]() 产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果
产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果![]() 产品的利润为300元/吨,
产品的利润为300元/吨, ![]() 产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
A. 14000元 B. 16000元 C. 18000元 D. 20000元
【答案】A
【解析】依题意,将题中数据统计如下表所示:
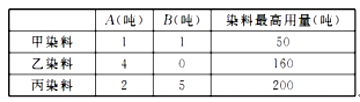
设该公司一天内安排生产![]() 产品
产品![]() 吨,
吨, ![]() 产品
产品![]() 吨,所获利润为
吨,所获利润为![]() 元.依据题意得目标函数为
元.依据题意得目标函数为![]() ,约束条件为
,约束条件为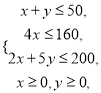 欲求目标函数
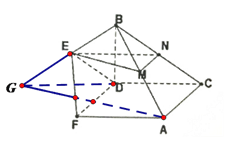
欲求目标函数![]() 的最大值,先画出约束条件表示的可行域,如图中阴影部分所示,则点
的最大值,先画出约束条件表示的可行域,如图中阴影部分所示,则点![]() ,
, ![]() ,
, ![]() ,
, ![]() , 作直线
, 作直线![]() ,当移动该直线过点
,当移动该直线过点![]() 时,
时, ![]() 取得最大值,则
取得最大值,则![]() 也取得最大值(也可通过代入凸多边形端点进行计算,比较大小求得).故
也取得最大值(也可通过代入凸多边形端点进行计算,比较大小求得).故![]() ,所以工厂每天生产
,所以工厂每天生产![]() 产品40吨,
产品40吨, ![]() 产品10吨时,才可获得最大利润,为14000元.选A.
产品10吨时,才可获得最大利润,为14000元.选A.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查,根据从其中随机抽取的50份调查问卷,得到了如下的列联表.
同意限定区域停车 | 不同意限定区域停车 | 合计 | |
男 | 18 | 7 | 25 |
女 | 12 | 13 | 25 |
合计 | 30 | 20 | 50 |
(1)学校计划在同意限定区域停车的家长中,按照分层抽样的方法,随机抽取5人在上学、放学期间在学校门口参与维持秩序,在随机抽取的5人中,选出2人担任召集人,求至少有一名女性的概率?
(2)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子,现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.