题目内容
(本小题满分12分)
已知半圆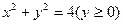 ,动圆与此半圆相切且与
,动圆与此半圆相切且与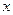 轴相切。
轴相切。
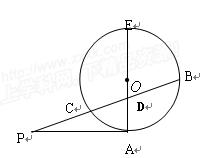
(1)求动圆圆心的轨迹,并画出其轨迹图形;
(2)是否存在斜率为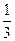 的直线
的直线 ,它与(1)中所得轨迹的曲线由左到右顺次交于A、B、C、D四点,且满足
,它与(1)中所得轨迹的曲线由左到右顺次交于A、B、C、D四点,且满足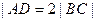 。若存在,求出
。若存在,求出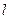 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
已知半圆
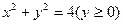 ,动圆与此半圆相切且与
,动圆与此半圆相切且与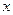 轴相切。
轴相切。(1)求动圆圆心的轨迹,并画出其轨迹图形;
(2)是否存在斜率为
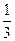 的直线
的直线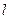 ,它与(1)中所得轨迹的曲线由左到右顺次交于A、B、C、D四点,且满足
,它与(1)中所得轨迹的曲线由左到右顺次交于A、B、C、D四点,且满足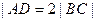 。若存在,求出
。若存在,求出 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。(1)动圆圆心的轨迹方程为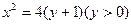 及
及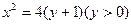
(2)这样的直线不存在
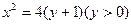 及
及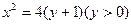
(2)这样的直线不存在
(1)设动圆圆心为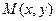 ,做
,做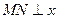 轴交
轴交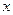 轴于N。 1分
轴于N。 1分
若两圆外切,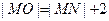 ,
,
所以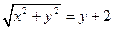 ,
,
化简得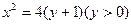 3分
3分
若两圆内切,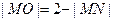 ,
,
所以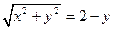 ,
,
化简得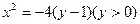 4分
4分
综上,动圆圆心的轨迹方程为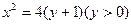
及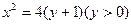 ,
,
其图象是两条抛物线位于 轴上方的部分,作简图如图: 6分
轴上方的部分,作简图如图: 6分
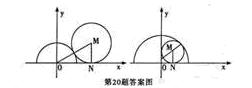
(2)设直线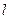 存在其方程可设为
存在其方程可设为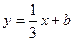 ,
,
依题意,它与曲线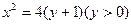 交于A,D,
交于A,D,
与曲线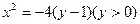 交于B,C 7分
交于B,C 7分
由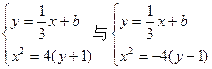
得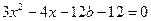 及
及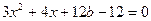 9分
9分
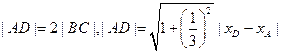
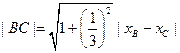 10分
10分
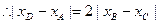
即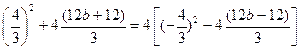 11分
11分
解得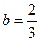 ,
,
将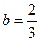 代入方程
代入方程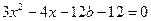
得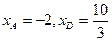
因为曲线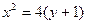 中横坐标范围为(-∞,-2)∪(2,+∞),
中横坐标范围为(-∞,-2)∪(2,+∞),
所以这样的直线不存在 12分
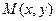 ,做
,做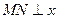 轴交
轴交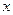 轴于N。 1分
轴于N。 1分若两圆外切,
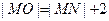 ,
,所以
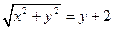 ,
,化简得
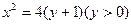 3分
3分若两圆内切,
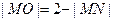 ,
,所以
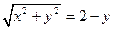 ,
,化简得
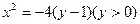 4分
4分综上,动圆圆心的轨迹方程为
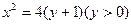
及
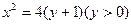 ,
,其图象是两条抛物线位于
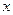 轴上方的部分,作简图如图: 6分
轴上方的部分,作简图如图: 6分
(2)设直线
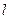 存在其方程可设为
存在其方程可设为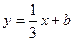 ,
,依题意,它与曲线
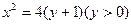 交于A,D,
交于A,D,与曲线
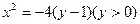 交于B,C 7分
交于B,C 7分由
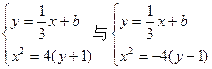
得
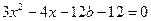 及
及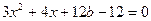 9分
9分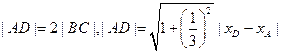
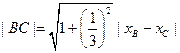 10分
10分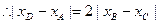
即
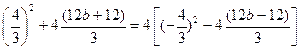 11分
11分解得
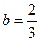 ,
,将
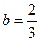 代入方程
代入方程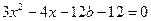
得
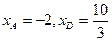
因为曲线
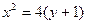 中横坐标范围为(-∞,-2)∪(2,+∞),
中横坐标范围为(-∞,-2)∪(2,+∞),所以这样的直线不存在 12分

练习册系列答案
相关题目
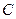 过点
过点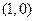 ,且圆心在
,且圆心在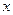 轴的正半轴上,直线
轴的正半轴上,直线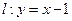 被该圆所截得的弦长为
被该圆所截得的弦长为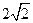 ,则圆
,则圆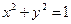 是位于第一象限的任意一点作圆的切线,则该切线与两坐标轴所围成的三角形面积的最小值是___________。
是位于第一象限的任意一点作圆的切线,则该切线与两坐标轴所围成的三角形面积的最小值是___________。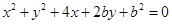 与x轴相切,则b的值为
与x轴相切,则b的值为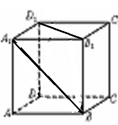
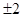
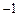 和3,在y轴上的一个截距为1.
和3,在y轴上的一个截距为1.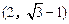 的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角.
的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角.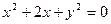 的圆心C,且与直线x+y=0垂直的直线方程是( )
的圆心C,且与直线x+y=0垂直的直线方程是( )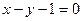
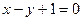
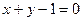
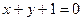
 知直线
知直线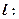
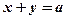 与圆
与圆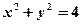 交于
交于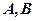 两点,且
两点,且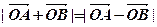 (其中O为坐标原点),则实数
(其中O为坐标原点),则实数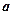 的值是 ( )
的值是 ( )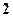
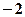
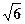 或
或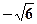
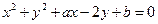 上,点P关于直线
上,点P关于直线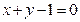 的对称点也在圆C上,则圆C的半径为 .
的对称点也在圆C上,则圆C的半径为 .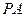 与圆
与圆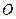 相切于
相切于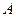 ,不过圆心
,不过圆心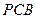 与直径
与直径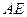 相交于
相交于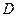 点.已知∠
点.已知∠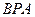 =
=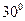 ,
,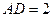 ,
,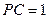 ,则圆
,则圆