题目内容
类比平面内 “垂直于同一条直线的两条直线互相平行”的性质,可推出空间下列结论:
①垂直于同一条直线的两条直线互相平行 ②垂直于同一个平面的两条直线互相平行
③垂直于同一条直线的两个平面互相平行 ④垂直于同一个平面的两个平面互相平行,则正确的结论是 ( )
| A.①② | B.②③ | C.③④ | D.①④ |
B
解析试题分析:在空间中,重直于同一条直线的两条直线也可能异面,也可能相交,如正方体的三条交于顶点的棱,所以①错;在空间中垂直于同一个平面的两个平面也可能相交也可能平行,如正方体中交于一顶点的三个面之间的关系,所以④错.所以选B.有关空间中点、线、面之间的位置关系的题一般是放在正方体中,得用正方体中的点、线、面关系来解决,更直观.
考点:1.空间中点、线、面之间的位置关系;2.空间想象能力.

练习册系列答案
相关题目
三棱柱 中,侧棱
中,侧棱 底面
底面 ,底面三角形
,底面三角形 是正三角形,
是正三角形,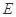 是
是 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )
A. 与 与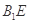 是异面直线 是异面直线 |
B. 平面 平面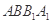 |
C.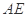 、 、 为异面直线,且 为异面直线,且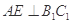 |
D. 平面 平面 |
设m,n是两条不同的直线,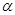 、
、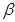 是两个不同的平面.则下列命题中正确的是( )
是两个不同的平面.则下列命题中正确的是( )
A.m⊥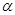 ,n ,n 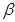 ,m⊥n ,m⊥n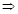 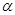 ⊥ ⊥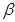 |
B.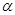 ⊥ ⊥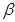 , ,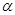 ∩ ∩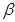 =m,n⊥m =m,n⊥m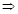 n⊥ n⊥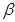 |
C.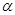 ⊥ ⊥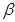 ,m⊥ ,m⊥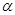 ,n∥ ,n∥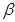 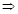 m⊥n m⊥n |
D.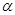 ∥ ∥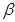 ,m⊥ ,m⊥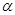 ,n∥ ,n∥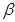 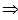 m⊥n m⊥n |
已知三条不重合的直线 和两个不重合的平面
和两个不重合的平面 ,下列命题正确的是( )
,下列命题正确的是( )
A.若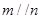 , , ,则 ,则 |
B.若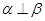 , , ,且 ,且 ,则 ,则 |
C.若 , , ,则 ,则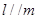 |
D.若 , ,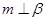 ,且 ,且 ,则 ,则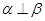 |
教室内有一把直尺,无论怎样放置,地面上总有这样的直线与该直尺所在直线 ( ).
| A.平行 | B.异面 | C.垂直 | D.相交但不垂直 |
设b,c表示两条直线,α,β表示两个平面,则下列命题正确的是( )
| A.若b?α,c∥α,则c∥b |
| B.若b?α,b∥c,则c∥α |
| C.若c?α,α⊥β,则c⊥β |
| D.若c?α,c⊥β,则α⊥β |
如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )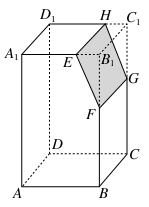
| A.EH∥FG |
| B.四边形EFGH是矩形 |
| C.Ω是棱柱 |
| D.Ω是棱台 |
[2013·湖南娄底5月]平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是( )
| A.AB∥CD | B.AD∥CB |
| C.AB与CD相交 | D.A,B,C,D四点共面 |
设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A.若α⊥β,m?α,n?β,则m⊥n |
| B.若α∥β,m?α,n?β,则m∥n |
| C.若m⊥n,m?α,n?β,则α⊥β |
| D.若m⊥α,m∥n,n∥β,则α⊥β |