题目内容
已知 为异面直线,
为异面直线,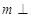 平面
平面 ,
, 平面
平面 .平面α与β外的直线
.平面α与β外的直线 满足
满足 ,则( )
,则( )
A. ,且 ,且 | B. ,且 ,且 |
C. 与 与 相交,且交线垂直于 相交,且交线垂直于 | D. 与 与 相交,且交线平行于 相交,且交线平行于 |
D
解析试题分析:若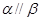 ,由
,由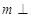 平面
平面 ,
, 平面
平面 得
得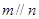 ,与
,与 为异面直线相矛盾,A错;若
为异面直线相矛盾,A错;若 ,且
,且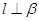 结合条件则
结合条件则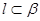 或
或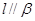 ,B错;若
,B错;若 与
与 相交结合条件可证交线平行于
相交结合条件可证交线平行于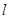 ,故选D。
,故选D。
考点:(1)线面平行、面面平行性质及判定定理的应用;(2)面面垂直性质及判定定理的应用。

练习册系列答案
相关题目
三棱柱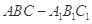 中,侧棱
中,侧棱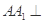 底面
底面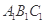 ,底面三角形
,底面三角形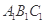 是正三角形,
是正三角形, 是
是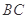 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )
A.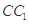 与 与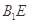 是异面直线 是异面直线 |
B.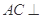 平面 平面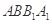 |
C. 、 、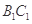 为异面直线,且 为异面直线,且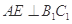 |
D.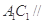 平面 平面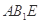 |
已知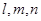 是三条不同的直线,
是三条不同的直线,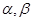 是两个不同的平面,下列命题为真命题的是( )
是两个不同的平面,下列命题为真命题的是( )
A.若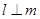 , , , , , ,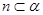 ,则 ,则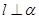 |
B.若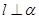 , ,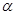 ∥ ∥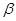 , ,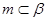 ,则 ,则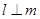 |
C.若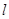 ∥ ∥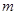 , , ,则 ,则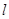 ∥ ∥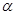 |
D.若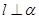 , ,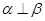 , ,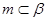 ,则 ,则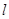 ∥ ∥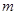 |
如图,在棱长为 的正方体
的正方体 中,
中, 为
为 的中点,
的中点,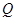 为
为 上任意一点,
上任意一点, 为
为 上两点,且
上两点,且 的长为定值,则下面四个值中不是定值的是( )
的长为定值,则下面四个值中不是定值的是( )
A.点 到平面 到平面 的距离 的距离 |
B.直线 与平面 与平面 所成的角 所成的角 |
C.三棱锥 的体积 的体积 |
D. 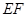 的面积 的面积 |
教室内有一把直尺,无论怎样放置,地面上总有这样的直线与该直尺所在直线 ( ).
| A.平行 | B.异面 | C.垂直 | D.相交但不垂直 |
设b,c表示两条直线,α,β表示两个平面,则下列命题正确的是( )
| A.若b?α,c∥α,则c∥b |
| B.若b?α,b∥c,则c∥α |
| C.若c?α,α⊥β,则c⊥β |
| D.若c?α,c⊥β,则α⊥β |
如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )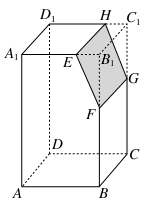
| A.EH∥FG |
| B.四边形EFGH是矩形 |
| C.Ω是棱柱 |
| D.Ω是棱台 |