题目内容
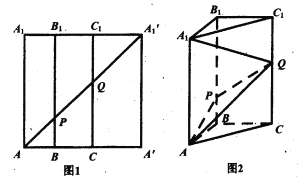
【题目】已知如图1所示,在边长为12的正方形![]() ,中,
,中,![]() ,且
,且![]() ,
,![]() 分别交
分别交![]() 于点
于点![]() ,将该正方形沿
,将该正方形沿![]() ,折叠,使得
,折叠,使得![]() 与
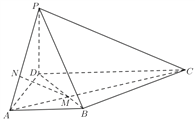
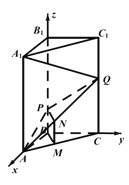
与![]() 重合,构成如图2 所示的三棱柱
重合,构成如图2 所示的三棱柱![]() ,在该三棱柱底边
,在该三棱柱底边![]() 上有一点
上有一点![]() ,满足
,满足![]() ; 请在图2 中解决下列问题:
; 请在图2 中解决下列问题:
(I)求证:当![]() 时,
时,![]() //平面
//平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
【答案】(I)见解析;(II)![]() 或
或![]() .
.
【解析】分析:(I)过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() ,推出四边形
,推出四边形![]() 为平行四边形,则
为平行四边形,则![]() ,由此能证明
,由此能证明![]() //平面
//平面![]() ;(Ⅱ)根据
;(Ⅱ)根据![]() 及正方形边长为
及正方形边长为![]() ,可推出
,可推出![]() ,从而以
,从而以![]() 为
为![]() 轴,建立空间直角坐标系,设立各点坐标,然后求出平面
轴,建立空间直角坐标系,设立各点坐标,然后求出平面![]() 的法向量,再根据直线
的法向量,再根据直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,即可求得
,即可求得![]() 的值.
的值.
详解:(I)解: 过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,所以
,所以![]() ,
,
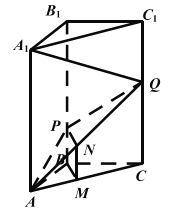
∴![]() 共面且平面
共面且平面![]() 交平面
交平面![]() 于
于![]() ,
,
∵![]()
又 ![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() //平面
//平面![]()
(II)解:∵![]()
∴![]() ,从而
,从而![]() ,即
,即![]() .
.
∴![]() .
.
分別以![]() 为
为![]() 轴,则
轴,则![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,所以
,所以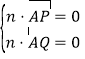 得
得![]() .
.
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]()
由![]() 得
得![]() 的坐标为
的坐标为![]()
∵直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,
,
∴解得![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】甲、乙、丙三人去某地务工,其工作受天气影响,雨天不能出工,晴天才能出工.其计酬方式有两种,方式一:雨天没收入,晴天出工每天![]() 元;方式而:雨天每天
元;方式而:雨天每天![]() 元,晴天出工每天
元,晴天出工每天![]() 元;三人要选择其中一种计酬方式,并打算在下个月(
元;三人要选择其中一种计酬方式,并打算在下个月(![]() 天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(
天)内的晴天都出工,为此三人作了一些调查,甲以去年此月的下雨天数(![]() 天)为依据作出选择;乙和丙在分析了当地近
天)为依据作出选择;乙和丙在分析了当地近![]() 年此月的下雨天数(
年此月的下雨天数(![]() )的频数分布表(见下表)后,乙以频率最大的
)的频数分布表(见下表)后,乙以频率最大的![]() 值为依据作出选择,丙以
值为依据作出选择,丙以![]() 的平均值为依据作出选择.
的平均值为依据作出选择.
| 8 | 9 | 10 | 11 | 12 | 13 |
频数 | 3 | 1 | 2 | 0 | 2 | 1 |
(Ⅰ)试判断甲、乙、丙选择的计酬方式,并说明理由;
(Ⅱ)根据统计范围的大小,你觉得三人中谁的依据更有指导意义?
(Ⅲ)以频率作为概率,求未来三年中恰有两年,此月下雨不超过![]() 天的概率.
天的概率.