题目内容
若关于x的方程ax+
=3的正实数解有且仅有一个,那么实数a的取值范围为( )
| 1 |
| x2 |
| A.a≤0 | B.a≤1 | C.a≤1或a=2 | D.a≤0或a=2 |
由函数解析式可得:x≠0,
如果关于x的方程 ax+
=3有且仅有一个正实数解,即方程ax3-3x2+1=0有且仅有一个正实数解,
构造函数f(x)=ax3-3x2+1,则函数f(x)的图象与x正半轴有且仅有一个交点.
又∵f'(x)=3x(ax-2)
①当a=0时,代入原方程知此时仅有一个正数解
满足要求;
②当a>0时,则得f(x)在(-∞,0)和(
,+∞)上单调递增,在(0,
)上单调递减,
f(0)=1,知若要满足条件只有x=2a时,f(x)取到极小值0,x=
入原方程得到正数解a=2,满足要求;
③当a<0时,同理f(x)在(-∞,
)和(0,+∞)上单调递减,在(
,0)上单调递增,
函数的极大值f(0)=1>0,f(x)=0有1正根,a<0满足条件
综上可得a≤0,a=2
故选:D
如果关于x的方程 ax+
| 1 |
| x2 |
构造函数f(x)=ax3-3x2+1,则函数f(x)的图象与x正半轴有且仅有一个交点.
又∵f'(x)=3x(ax-2)
①当a=0时,代入原方程知此时仅有一个正数解
| 3 |
②当a>0时,则得f(x)在(-∞,0)和(
| 2 |
| a |
| 2 |
| a |
f(0)=1,知若要满足条件只有x=2a时,f(x)取到极小值0,x=
| 2 |
| a |
③当a<0时,同理f(x)在(-∞,
| 2 |
| a |
| 2 |
| a |
函数的极大值f(0)=1>0,f(x)=0有1正根,a<0满足条件
综上可得a≤0,a=2
故选:D

练习册系列答案
相关题目
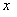 的方程
的方程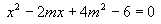 两根为
两根为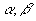 ,试求
,试求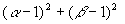 的极值。
的极值。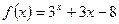 ,用二分法求方程
,用二分法求方程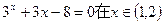 内近似解的过程中得
内近似解的过程中得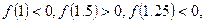 则方程的根落在区间
则方程的根落在区间