题目内容
函数f(x)=|x-1|+|x-a|,
(1)若a=-1,解不等式f(x)≥3;
(2)如果对?x∈R时f(x)≥2都成立,求a的取值范围.
(1)若a=-1,解不等式f(x)≥3;
(2)如果对?x∈R时f(x)≥2都成立,求a的取值范围.
(1)当a=1时,f(x)=|x-1|+|x+1|,由f(x)≥3得|x-1|+|x+1|≥3,由绝对值几何意义知不等式的解集为{x|x≤-
或x≥
},(5分)
(2)若a=1,则f(x)=2|x-1|不满足题设条件.
若a<1,f(x)=
,f(x)的最小值为1-a;(8分)
a>1,f(x)=
,f(x)的最小值a-1.(11分)
所以对于?x∈Rf(x)≥2的充要条件是|a-1|≥2,从而a的取值范围(-∞,-1]∪[3,+∞).(12分)
| 3 |
| 2 |
| 3 |
| 2 |
(2)若a=1,则f(x)=2|x-1|不满足题设条件.
若a<1,f(x)=
|
a>1,f(x)=
|
所以对于?x∈Rf(x)≥2的充要条件是|a-1|≥2,从而a的取值范围(-∞,-1]∪[3,+∞).(12分)

练习册系列答案
相关题目

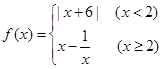 ,使不等式
,使不等式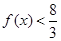 成立的
成立的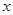 的取值范围是__________.
的取值范围是__________. 1,2,3,4,5,6时,比较
1,2,3,4,5,6时,比较 和
和 的大小并猜想( )
的大小并猜想( ) 时,
时,
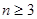 时,
时, 时,
时, 时,
时, 的解集为 。
的解集为 。