题目内容
若存在实数x满足不等式|x-3|+|x-5|<m2-m,则实数m的取值范围为______.
∵存在实数x满足不等式|x-3|+|x-5|<m2-m,∴m2-m应大于|x-3|+|x-5|的最小值.
而由绝对值的意义可得|x-3|+|x-5|表示数轴上的x对应点到3和5对应点的距离之和,其最小值为2,
∴m2-m>2,解得 m<-1,或 m>2,
故实数m的取值范围为 (-∞,-1)∪(2,+∞).
故答案为(-∞,-1)∪(2,+∞)
而由绝对值的意义可得|x-3|+|x-5|表示数轴上的x对应点到3和5对应点的距离之和,其最小值为2,
∴m2-m>2,解得 m<-1,或 m>2,
故实数m的取值范围为 (-∞,-1)∪(2,+∞).
故答案为(-∞,-1)∪(2,+∞)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
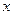 , 若不等式
, 若不等式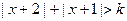 恒成立, 则实数
恒成立, 则实数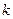 的取值范围是( )
的取值范围是( )  ,那么下列不等式一定成立的是( )
,那么下列不等式一定成立的是( )

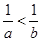

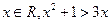 ”的否定是“任意
”的否定是“任意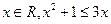 ”;
”;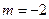 ”是“直线
”是“直线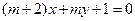 与直线
与直线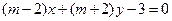 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;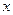 的不等式
的不等式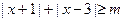 的解集为
的解集为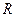 ,则
,则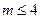 .
. 使不等式
使不等式 在
在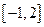 成立,则
成立,则