题目内容
已知函数f(x)=|2x+2|+|2x-3|.
(Ⅰ)若?x∈R,使得不等式f(x)<m成立,求m的取值范围;
(Ⅱ)求使得等式f(x)≤|4x-1|成立的x的取值范围.
(Ⅰ)若?x∈R,使得不等式f(x)<m成立,求m的取值范围;
(Ⅱ)求使得等式f(x)≤|4x-1|成立的x的取值范围.
(Ⅰ)∵f(x)=|2x+2|+|2x-3|=2(|x+1|+|x-
|)≥2|(x+1)-(x-
)|=5,
∴使得不等式f(x)<m成立的m的取值范围是(5,+∞).
(Ⅱ)由f(x)=|2x+2|+|2x-3|≥|2x+2+2x-3|=|4x-1|,
∴不等式f(x)≤|4x-1|即|2x+2|+|2x-3|=|4x-1|,当且仅当(2x+2)(2x-3)≥0时取等号,
即当x≤-1,或x≥
时,|2x+2|+|2x-3|=|4x-1|,
∴x的取值范围是(-∞,-1]∪[
+∞).
| 3 |
| 2 |
| 3 |
| 2 |
∴使得不等式f(x)<m成立的m的取值范围是(5,+∞).
(Ⅱ)由f(x)=|2x+2|+|2x-3|≥|2x+2+2x-3|=|4x-1|,
∴不等式f(x)≤|4x-1|即|2x+2|+|2x-3|=|4x-1|,当且仅当(2x+2)(2x-3)≥0时取等号,
即当x≤-1,或x≥
| 3 |
| 2 |
∴x的取值范围是(-∞,-1]∪[
| 3 |
| 2 |

练习册系列答案
相关题目
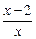 >0},则A∩B等于
>0},则A∩B等于 若
若 ,则
,则 的取值范围是 .
的取值范围是 . ,那么下列不等式一定成立的是( )
,那么下列不等式一定成立的是( )

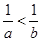

 则( )
则( ) 



 的解集是
的解集是