题目内容
(14分)数列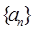 中,
中, ,
, 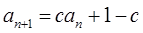
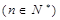
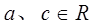
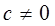
(1)求证: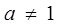 时,
时,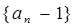 是等比数列,并求
是等比数列,并求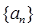 通项公式。
通项公式。
(2)设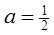 ,
,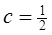 ,
,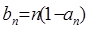
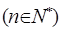 求:数列
求:数列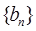 的前n项的和
的前n项的和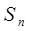 。
。
(3)设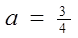 、
、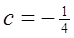 、
、
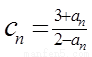 。记
。记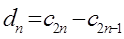 ,数列
,数列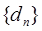 的前n项和
的前n项和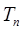 。证明:
。证明: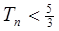
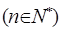 。
。
【答案】
(1)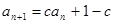
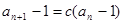
 。;(2)
。;(2)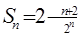 ;(3)
;(3)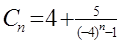 ,
,
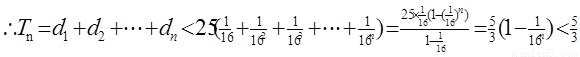 【解析】
【解析】
试题分析:(1)证明: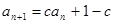
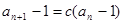
 。
。


(2)由(1)的

由错位相减法得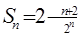
(3)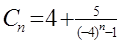

 考点:数列通项公式的求法;等比数列的性质;数列前n项和的求法。
考点:数列通项公式的求法;等比数列的性质;数列前n项和的求法。
点评:若已知递推公式为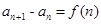 的形式求通项公式常用累加法。
的形式求通项公式常用累加法。
注:①若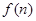 是关于n的一次函数,累加后可转化为等差数列求和;
是关于n的一次函数,累加后可转化为等差数列求和;
②若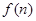 是关于n的二次函数,累加后可分组求和;
是关于n的二次函数,累加后可分组求和;
③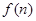 是关于n的指数函数,累加后可转化为等比数列求和;
是关于n的指数函数,累加后可转化为等比数列求和;
④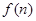 是关于n的分式函数,累加后可裂项求和。
是关于n的分式函数,累加后可裂项求和。

练习册系列答案
相关题目