题目内容
【题目】通过研究学生的学习行为,心理学家发现,学生接受能力依赖于老师引入概念和描述问题所用的时间,讲座开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用![]() 表示学生掌握和接受概念的能力(
表示学生掌握和接受概念的能力(![]() 的值越大,表示接受能力越强),
的值越大,表示接受能力越强),![]() 表示提出和讲授概念的时间(单位:分),可以有以下公式:
表示提出和讲授概念的时间(单位:分),可以有以下公式: 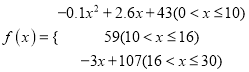 .
.
(1)开讲多少分钟后,学生的接受能力最强?能维持多少分钟?
(2)开讲5分钟与开讲20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题,需要55的接受能力以及13分钟的时间,老师能否及时在学生一直达到所需接受能力的状态下讲授完这个难题?
【答案】(1)能维持6分钟时间(2)开讲5分钟时学生的接受能力比开讲20分钟时要强一些(3)来不及
【解析】试题分析:(1)当![]() 时,函数为二次函数,对称轴为
时,函数为二次函数,对称轴为![]() ,开口向下故在这个区间上单调递增,当
,开口向下故在这个区间上单调递增,当![]() 时取得最大值为
时取得最大值为![]() .当
.当![]() 时,函数为减函数,且
时,函数为减函数,且![]() ,故开讲
,故开讲![]() 分钟后达到最大值,维持
分钟后达到最大值,维持![]() 分钟.(2)通过比较
分钟.(2)通过比较![]() 的值可知开讲
的值可知开讲![]() 分钟时接受能力更强.(3)在区间
分钟时接受能力更强.(3)在区间![]() 上分别令函数值为
上分别令函数值为![]() ,求得对应的时间,作差后可知老师来不及讲授完.
,求得对应的时间,作差后可知老师来不及讲授完.
试题解析:
(1)当![]() 时,
时, ![]()
故![]() 在
在![]() 时递增,最大值为
时递增,最大值为![]()
当![]() 时,
时, ![]()
当![]() 时,
时, ![]() 为减函数,且
为减函数,且![]()
因此,开讲10分钟后,学生达到最强接受能力(为59),能维持6分钟时间.
(2)![]()
![]()
故开讲5分钟时学生的接受能力比开讲20分钟时要强一些
(3)当![]() 时,令
时,令![]() ,解得
,解得![]() 或20(舍)
或20(舍)
当![]() 时,令
时,令![]() ,解得
,解得![]()
因此学生达到(含超过)55的接受能力的时间为![]() (分)
(分)
老师来不及在学生一直达到所需接受能力的状态下讲授完这个难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目