题目内容
12.已知函数f(x)=sinx-2$\sqrt{3}$sin2$\frac{x}{2}$.f(x)的最小值是-2-$\sqrt{3}$.分析 运用三角函数的公式得出f(x)=2sin(x+$\frac{π}{3}$)-$\sqrt{3}$,结合正弦函数的性质求解即可.
解答 解:∵函数f(x)=sinx-2$\sqrt{3}$sin2$\frac{x}{2}$=sinx+$\sqrt{3}$cosx$-\sqrt{3}$
∴f(x)=2sin(x+$\frac{π}{3}$)-$\sqrt{3}$
∵-1≤sin(x$+\frac{π}{3}$)≤1,
∴-2-$\sqrt{3}$≤2sin(x+$\frac{π}{3}$)-$\sqrt{3}$$≤2-\sqrt{3}$
故答案为:-2-$\sqrt{3}$.
点评 本题考查了三角函数的图象和性质,属于简单的复合函数的运用问题,属于中档题,关键是变形得出f(x)=2sin(x+$\frac{π}{3}$)-$\sqrt{3}$

练习册系列答案
相关题目
3.如图,在复平面内,复数z1和z2对应的点分别是A和B,则$\frac{{z}_{1}}{{z}_{2}}$等于( )
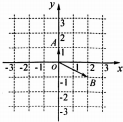

| A. | $\frac{1}{5}$+$\frac{2}{5}$i | B. | $\frac{2}{5}$+$\frac{1}{5}$i | C. | -$\frac{1}{5}$+$\frac{2}{5}$i | D. | -$\frac{2}{5}$+$\frac{1}{5}$i |