题目内容
17.某建筑公司计划450万元购买甲型与乙型两款挖土机,购买总数不超过50辆,其中购买甲型挖土机需要13万元/辆,购买乙型挖土机需要8万元/辆,假设甲型挖土机的纯利是2万元/辆,乙型挖土机的纯利润是1.5万元/辆,为了利润最大化,要如何购买两种挖土机?分析 设购买甲型挖土机x辆,乙型挖土机y辆;利润为z万元,从而得到约束条件及目标函数,由线性规划解答即可.
解答 解:设购买甲型挖土机x辆,乙型挖土机y辆;利润为z万元,
由题意得约束条件及目标函数如下,
$\left\{\begin{array}{l}{x+y≤50}\\{13x+8y≤450}\\{x∈N}\\{y∈N}\end{array}\right.$,
z=2x+1.5y,化简可得y=-$\frac{4}{3}$x+$\frac{2}{3}$z,
由题意作图象如下,
解$\left\{\begin{array}{l}{x+y=50}\\{13x+8y=450}\end{array}\right.$得$\left\{\begin{array}{l}{x=10}\\{y=40}\end{array}\right.$,
故为了利润最大化,要购买甲型挖土机10辆,乙型挖土机40辆.
点评 本题考查了线性规划在实际问题中的应用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
5.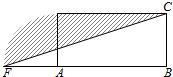 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
 设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )
设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于( )| A. | (4π+8)cm2 | B. | (4π+16)cm2 | C. | (3π+8)cm2 | D. | (3π+16)cm2 |
6.若a=log5$\frac{2}{3}$,b=log8$\sqrt{3}$,c=$\frac{1}{2}$log2$\sqrt{2}$,则a,b,c的大小关系是( )
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | c<b<a |