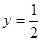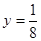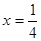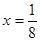题目内容
抛物线 上一点
上一点 到其焦点的距离为5.
到其焦点的距离为5.
(1)求 与
与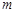 的值;
的值;
(2)若直线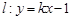 与抛物线
与抛物线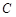 相交于
相交于 、
、 两点,
两点, 、
、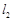 分别是该抛物线在
分别是该抛物线在 、
、 两点处的切线,
两点处的切线, 、
、 分别是
分别是 、
、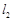 与该抛物线的准线交点,求证:
与该抛物线的准线交点,求证:
 上一点
上一点 到其焦点的距离为5.
到其焦点的距离为5.(1)求
 与
与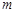 的值;
的值; (2)若直线
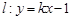 与抛物线
与抛物线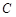 相交于
相交于 、
、 两点,
两点, 、
、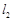 分别是该抛物线在
分别是该抛物线在 、
、 两点处的切线,
两点处的切线, 、
、 分别是
分别是 、
、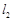 与该抛物线的准线交点,求证:
与该抛物线的准线交点,求证:
(1)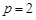 ,
,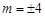 ;(2)见解析.
;(2)见解析.
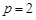 ,
,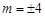 ;(2)见解析.
;(2)见解析.本试题主要是考查了抛物线的定义的运用,以及运用直线与抛物线联立方程组,求解两根的和,两根积的关系式,同时能求解抛物线上过一点的切线房产概念,利用坐标法求解解析几何的问题。
解:(1)根据抛物线定义,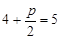 ,解得
,解得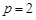 …………(2分)
…………(2分)
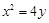 ,将
,将 代入
代入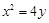 ,解得
,解得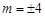 …………(4分)
…………(4分)
(2)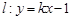 带入
带入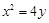 得
得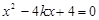 ,
,
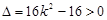 ,
,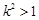 ,
,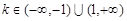 , …………(5分)
, …………(5分)
设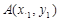 ,
,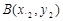 ,则
,则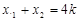 ,
,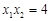
由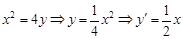 ,所以抛物线在
,所以抛物线在 处的切线
处的切线 的方程为
的方程为
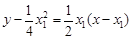 ,即
,即 .
.
令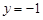 ,得
,得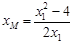 . …………(6分)
. …………(6分)
同理,得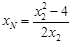 .
.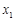 、
、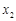 是方程①的两个实根,故
是方程①的两个实根,故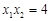 ,即
,即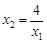 ,
,
从而有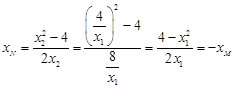 …………(8分)
…………(8分)
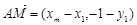 ,
,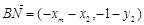 ,
,
方法1:∵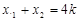 ,
,
∴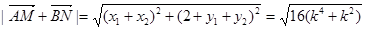 , …………(10分)
, …………(10分)
∵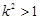 ,∴
,∴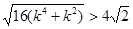 ,即
,即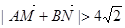 .
.
…………(12分)
方法2:
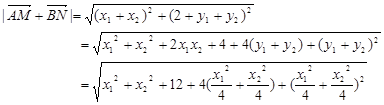 ,
,
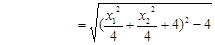 …………(10分)
…………(10分)
∵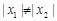 ,
,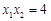 ,∴
,∴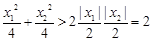
∴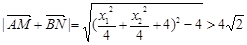 . ………………..(12分)
. ………………..(12分)
解:(1)根据抛物线定义,
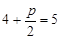 ,解得
,解得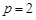 …………(2分)
…………(2分)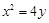 ,将
,将 代入
代入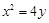 ,解得
,解得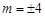 …………(4分)
…………(4分)(2)
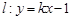 带入
带入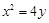 得
得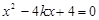 ,
,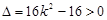 ,
,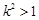 ,
,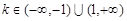 , …………(5分)
, …………(5分)设
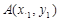 ,
,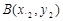 ,则
,则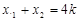 ,
,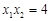
由
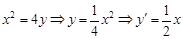 ,所以抛物线在
,所以抛物线在 处的切线
处的切线 的方程为
的方程为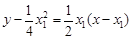 ,即
,即 .
.令
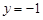 ,得
,得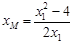 . …………(6分)
. …………(6分)同理,得
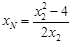 .
.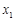 、
、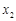 是方程①的两个实根,故
是方程①的两个实根,故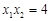 ,即
,即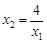 ,
,从而有
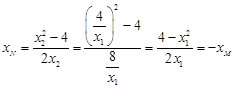 …………(8分)
…………(8分)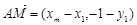 ,
,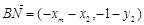 ,
,方法1:∵
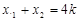 ,
,
∴
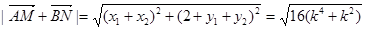 , …………(10分)
, …………(10分)∵
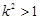 ,∴
,∴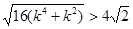 ,即
,即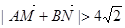 .
.…………(12分)
方法2:
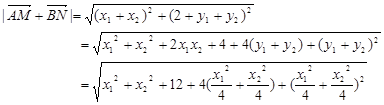 ,
,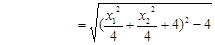 …………(10分)
…………(10分)∵
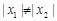 ,
,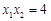 ,∴
,∴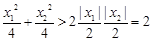
∴
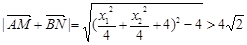 . ………………..(12分)
. ………………..(12分)
练习册系列答案
相关题目
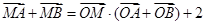 .
.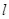 经过抛物线
经过抛物线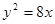 的焦点
的焦点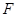 ,且与抛物线相交于
,且与抛物线相交于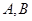 两点,求线段
两点,求线段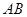 的长。
的长。 与点F的距离为4,则抛物线方程为 .
与点F的距离为4,则抛物线方程为 .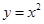 的焦点坐标是
的焦点坐标是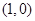
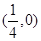
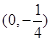
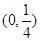
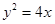 上一点
上一点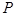 引抛物线准线的垂线,垂足为
引抛物线准线的垂线,垂足为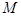 ,且
,且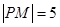 ,设抛物线的焦点为
,设抛物线的焦点为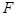 ,则
,则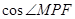 = .
= .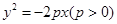 上,则它的边长为( )
上,则它的边长为( )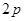


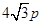
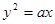 的准线是直线
的准线是直线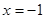 ,那么它的焦点坐标是 ( )
,那么它的焦点坐标是 ( )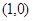



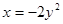 的准线方程是
的准线方程是