题目内容
已知椭圆
：
(
)过点
，其左、右焦点分别为
，且
．
（1）求椭圆的方程；
（2）若
是直线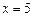
上的两个动点，且
，则以
为直径的圆
是否过定点？请说明理由．
（1）
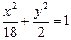
（2）过点（8，0）和（2，0）
解析
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
口算题卡加应用题集训系列答案综合自测系列答案题目内容
已知椭圆：()过点，其左、右焦点分别为，且．
（1）求椭圆的方程；
（2）若是直线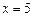上的两个动点，且，则以为直径的圆是否过定点？请说明理由．
（1）
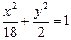
（2）过点（8，0）和（2，0）
解析
口算题卡加应用题集训系列答案综合自测系列答案
|=4，|
|=3，（2
的夹角θ；
，求以
为邻边的平行四边形的两条对角线的长度.
，
，其中
，
，
及
的值；
与
的夹角的正弦值.
(a>b>0)经过点M(
，1)，离心率为
．
，试问直线AB是否恒过定点，若恒过定点，请给出证明，并求出该定点的坐标；若不过，请说明理由．
，
，对任意
都有
.
的最小值；
,使
⊥
；
且
⊥
，试求出k关于t的关系式k=f(t).
．
，且
，求角
的值；
，求
的值．
，
,
的夹角为60o, 
, 
,当实数
为何值时，⑴
∥
⑵