题目内容
20. 在正方体ABCD-A1B1C1D1中,其棱长为a.
在正方体ABCD-A1B1C1D1中,其棱长为a.(1)求证:BD1⊥面AB1C;
(2)求点B到面AB1C的距离.
分析 (1)利用线面垂直的判定与性质,证明AC⊥BD1,AB1⊥BD1,即可证得结论;
(2)根据正方体ABCD-A1B1C1D1的棱长为a,算出三棱锥B1-ABC的体积为$\frac{1}{6}$a3,正三角形AB1C的面积为$\frac{\sqrt{3}}{2}$a2,由此利用等体积转换得${V}_{三棱锥{B}_{1}-ABC}$=${V}_{{三棱锥B-AB}_{1}C}$=$\frac{1}{6}$a2,建立关于d的等式即可解出B到平面AB1C的距离.
解答 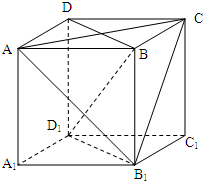 (1)证明:正方体ABCD-A1B1C1D1中
(1)证明:正方体ABCD-A1B1C1D1中
因为AC⊥BD,AC⊥DD1,且BD∩DD1
所以AC⊥平面BDD1B1
又BD1?平面BDD1B1
所以AC⊥BD1,同理可证AB1⊥BD1,
又因为AC与AB1是平面ACB1内的两条相交直线,
所以BD1⊥平面ACB1.
(2)解:∵正方体ABCD-A1B1C1D1的棱长为a
∴三棱锥B1-ABC的体积为
V=$\frac{1}{3}$S△ABC•BB1=$\frac{1}{3}$×$\frac{1}{2}$a2×a=$\frac{1}{6}$a3.
∵正三角形AB1C的边长为$\sqrt{2}$a,
∴${S}_{{△AB}_{1}C}$=$\frac{\sqrt{3}}{4}$•($\sqrt{2}$a)2=$\frac{\sqrt{3}}{2}$a2.
设点B到平面AB1C的距离为d,
则${V}_{三棱锥{B}_{1}-ABC}$=${V}_{{三棱锥B-AB}_{1}C}$=$\frac{1}{6}$a3,
即$\frac{1}{3}$×${S}_{{△AB}_{1}C}$×d=$\frac{1}{5}$a3,得$\frac{\sqrt{3}}{6}$a2d=$\frac{1}{6}$a3,解之得d=$\frac{\sqrt{3}}{3}$a,
即点B到平面AB1C的距离为$\frac{\sqrt{3}}{3}$a.
点评 本题考查线面垂直,考查三棱锥体积公式,求点B到平面AB1C的距离.着重考查了正方体的性质、正三角形面积公式和利用等体积转换的方法求点面距离等知识,属于中档题.

 优生乐园系列答案
优生乐园系列答案| A. | 奇函数,且在定义域内单调递减 | |
| B. | 奇函数,且在定义域内单调递增 | |
| C. | 非奇非偶函数,且在(0,+∞)上单调递增 | |
| D. | 偶函数,且在(0,+∞)上单调递增 |