题目内容
8.证明:$\frac{2}{{3}^{1}-1}$+$\frac{2}{{3}^{2}-1}$+…+$\frac{2}{{3}^{n}-1}$<$\frac{3}{2}$(n∈N*)分析 当n≥3时,$\frac{2}{{3}^{n}-1}<\frac{2}{3×{2}^{n}}$,再利用等比数列的前n项和公式即可得出.
解答 证明:∵当n≥3时,$\frac{2}{{3}^{n}-1}<\frac{2}{3×{2}^{n}}$,
∴当n≥3时,$\frac{2}{{3}^{1}-1}$+$\frac{2}{{3}^{2}-1}$+…+$\frac{2}{{3}^{n}-1}$<1+$\frac{1}{4}$+$\frac{2}{3}$$(\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}+…+\frac{1}{{2}^{n}})$=$\frac{5}{4}$+$\frac{2}{3}×\frac{\frac{1}{8}(1-\frac{1}{{2}^{n-2}})}{1-\frac{1}{2}}$<$\frac{5}{4}$+$\frac{1}{6}$=$\frac{17}{12}$<$\frac{18}{12}$=$\frac{3}{2}$.
当n=1,2时,显然成立.
∴$\frac{2}{{3}^{1}-1}$+$\frac{2}{{3}^{2}-1}$+…+$\frac{2}{{3}^{n}-1}$<$\frac{3}{2}$(n∈N*).
点评 本题考查了等比数列的前n项和公式、“放缩法”、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目

 在正方体ABCD-A1B1C1D1中,其棱长为a.
在正方体ABCD-A1B1C1D1中,其棱长为a.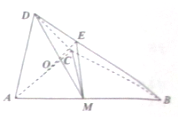 如图,△ACB,△ADC都为等腰直角三角形,M、O为AB、AC的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2.
如图,△ACB,△ADC都为等腰直角三角形,M、O为AB、AC的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2.