题目内容
5.已知圆C1:(x-a)2+y2=9,圆C2:(x-2)2+y2=4,以点C1、C2与A(0,2)围成的三角形的面积为5,求a的值.分析 确定圆心的坐标,利用以点C1、C2与A(0,2)围成的三角形的面积为5,求a的值.
解答 解:由题意,C1(a,0)、C2(2,0),
∵以点C1、C2与A(0,2)围成的三角形的面积为5,
∴$\frac{1}{2}$•|a-2|•2=5,
∴a=7或-3.
点评 本题考查圆的方程,三角形面积的计算,确定圆的圆心是关键.

练习册系列答案
相关题目
10.函数y=tan|x|的图象( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 以上答案都不对 |
1.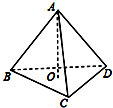 在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )
在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )
 在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )
在三棱锥A-BCD中,已知AB⊥CD,BC⊥AD,如图所示,则点A在平面BCD内的射影O是△BCD( )| A. | 三条中线的交点 | B. | 三角平分线的交点 | ||
| C. | 三条高线的交点 | D. | 三垂直平分线的交点 |

 在正方体ABCD-A1B1C1D1中,其棱长为a.
在正方体ABCD-A1B1C1D1中,其棱长为a.