题目内容
9.已知定义在R上的函数f(x)满足:f(x)=$\left\{\begin{array}{l}{{x}^{2}+2,x∈[0,1)}\\{2-{x}^{2},x∈[-1,0)}\end{array}\right.$且f(x+2)=f(x),g(x)=$\frac{2x+5}{x+2}$,则方程f(x)=g(x)在区间[-5,1]上的所有实根之和为( )| A. | -7 | B. | -8 | C. | -9 | D. | -10 |
分析 化简g(x)的表达式,得到g(x)的图象关于点(-2,1)对称,由f(x)的周期性,画出f(x),g(x)的图象,通过图象观察[-5,1]上的交点的横坐标的特点,求出它们的和.
解答 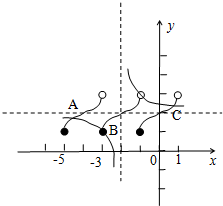 解:由题意知g(x)=$\frac{2x+5}{x+2}$,且函数f(x)的周期为2,
解:由题意知g(x)=$\frac{2x+5}{x+2}$,且函数f(x)的周期为2,
则函数f(x),g(x)在区间[-5,1]上的图象如下图所示:
由图形可知函数f(x),g(x)在区间[-5,1]上的交点为A,B,C,易知点B的横坐标为-3,
若设C的横坐标为t(0<t<1),则点A的横坐标为-4-t,
所以方程f(x)=g(x)在区间[-5,1]上的所有实数根之和为-3+(-4-t)+t=-7,
故选:A.
点评 本题考查分段函数的图象和运用,考查函数的周期性、对称性和应用,同时考查数形结合的能力,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 在正方体ABCD-A1B1C1D1中,其棱长为a.
在正方体ABCD-A1B1C1D1中,其棱长为a. 如图,△ACB,△ADC都为等腰直角三角形,M、O为AB、AC的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2.
如图,△ACB,△ADC都为等腰直角三角形,M、O为AB、AC的中点,且平面ADC⊥平面ACB,AB=4,AC=2$\sqrt{2}$,AD=2.