题目内容
11.a,b,c,d∈R+,设S=$\frac{a}{a+b+d}$+$\frac{b}{b+c+a}$+$\frac{c}{c+d+b}$+$\frac{d}{d+a+c}$,则下列判断中正确的是( )| A. | 0<S<1 | B. | 3<S<4 | C. | 2<S<3 | D. | 1<S<2 |
分析 利用已知可得:S>$\frac{a}{a+b+c+d}$+$\frac{b}{a+b+c+d}$+$\frac{c}{a+b+c+d}$+$\frac{d}{a+b+c+d}$=1;S<$\frac{a+c}{a+b+c+d}$+$\frac{b+d}{a+b+c+d}$+$\frac{c+a}{a+b+c+d}$+$\frac{b+d}{a+b+c+d}$=2,即可判断出.
解答 解:∵a,b,c,d∈R+,S=$\frac{a}{a+b+d}$+$\frac{b}{b+c+a}$+$\frac{c}{c+d+b}$+$\frac{d}{d+a+c}$,
∴S>$\frac{a}{a+b+c+d}$+$\frac{b}{a+b+c+d}$+$\frac{c}{a+b+c+d}$+$\frac{d}{a+b+c+d}$=1;
S<$\frac{a+c}{a+b+c+d}$+$\frac{b+d}{a+b+c+d}$+$\frac{c+a}{a+b+c+d}$+$\frac{b+d}{a+b+c+d}$=2,
∴1<S<2.
故选:D.
点评 本题考查了代数式的运算化简、放缩法、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知f(x)=ex,x∈R,a<b,记A=f(b)-f(a),B=$\frac{1}{2}$(b-a)(f(a)+f(b)),则A,B的大小关系是( )
| A. | A>B | B. | A≥B | C. | A<B | D. | A≤B |
16.在△ABC中,角A,B,C的对边分别为a,b,c,角A,B,C成等差数列,若$a=1,b=\sqrt{3}$,则c等于( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{3}$ |
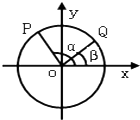 如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q,已知点P的坐标为$(-\frac{3}{5},\frac{4}{5})$.
如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q,已知点P的坐标为$(-\frac{3}{5},\frac{4}{5})$.