题目内容
6.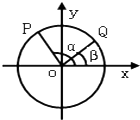 如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q,已知点P的坐标为$(-\frac{3}{5},\frac{4}{5})$.
如图,以Ox为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q,已知点P的坐标为$(-\frac{3}{5},\frac{4}{5})$.(Ⅰ)求$\frac{{2sinαcosα+2{{cos}^2}α}}{1+tanα}$的值;
(Ⅱ)若$\overrightarrow{OP}•\overrightarrow{OQ}=0$,求sinβ,cosβ,tanβ的值.
分析 (Ⅰ)由题意,sinα=$\frac{4}{5}$,cosα=-$\frac{3}{5}$,tanα=-$\frac{4}{3}$,即可求$\frac{{2sinαcosα+2{{cos}^2}α}}{1+tanα}$的值;
(Ⅱ)若$\overrightarrow{OP}•\overrightarrow{OQ}=0$,则sinβ=sin(α-90°)=-cosα=$\frac{3}{5}$,cosβ=cos(α-90°)=sinα=$\frac{4}{5}$,tanβ=$\frac{3}{4}$.
解答 解:(Ⅰ)由题意,sinα=$\frac{4}{5}$,cosα=-$\frac{3}{5}$,tanα=-$\frac{4}{3}$,
∴$\frac{{2sinαcosα+2{{cos}^2}α}}{1+tanα}$=$\frac{2×\frac{4}{5}×(-\frac{3}{5})+2×(-\frac{3}{5})^{2}}{1-\frac{4}{3}}$=$\frac{18}{25}$;
(Ⅱ)若$\overrightarrow{OP}•\overrightarrow{OQ}=0$,则sinβ=sin(α-90°)=-cosα=$\frac{3}{5}$,cosβ=cos(α-90°)=sinα=$\frac{4}{5}$,tanβ=$\frac{3}{4}$.
点评 本题考查任意角的三角函数的定义,考查诱导公式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
14.下列集合中表示空集的是( )
| A. | {x∈R|x+5=5} | B. | {x∈R|x+5>5} | C. | {x∈R|x2=0} | D. | {x∈R|x2+x+1=0} |
11.a,b,c,d∈R+,设S=$\frac{a}{a+b+d}$+$\frac{b}{b+c+a}$+$\frac{c}{c+d+b}$+$\frac{d}{d+a+c}$,则下列判断中正确的是( )
| A. | 0<S<1 | B. | 3<S<4 | C. | 2<S<3 | D. | 1<S<2 |
18.为了美化校园环境,某校计划对学生乱扔垃圾现象进行罚款处理,为了更好的了解学生的态度,随机抽取了200人进行了调查,得到如下数据:
(Ⅰ)若乱扔垃圾的人数 y 与罚款金额 x 满足线性回归方程,求回归方程$\hat y=bx+a$,其中b=-3.4,a=$\overline{y}$-b$\overline{x}$,并据此分析,要使乱扔垃圾者不超过20%,罚款金额至少是多少元?
(Ⅱ)若以调查数据为基础,从这5种罚款金额中随机抽取2种不同的数额,求这两种金额之和不低于25元的概率.
| 罚款金额x(单位:元) | 0 | 5 | 10 | 15 | 20 |
| 会继续乱扔垃圾的人数y | 80 | 50 | 40 | 20 | 10 |
(Ⅱ)若以调查数据为基础,从这5种罚款金额中随机抽取2种不同的数额,求这两种金额之和不低于25元的概率.
15.△ABC中,A(-5,0),B(5,0),点C在双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$上,则$\frac{sinA-sinB}{sinC}$=( )
| A. | $\frac{3}{5}$ | B. | $±\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | ±$\frac{4}{5}$ |