[题目]甲.乙两运动员进行射击训练.已知他们击中的环数都稳定在7.8.9.10环.且每次射击成绩互不影响．射击环数的频率分布条形图如下:若将频率视为概率.回答下列问题:(1)求甲运动员在3次射击中至少有1次击中9环以上的概率,(2)若甲.乙两运动员各自射击1次.表示这2次射击中击中9环以上的次数.求的分布列及期望．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】甲、乙两运动员进行射击训练，已知他们击中的环数都稳定在7，8，9，10环，且每次射击成绩互不影响．射击环数的频率分布条形图如下：

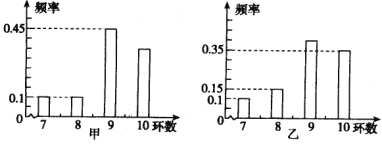
若将频率视为概率，回答下列问题：

(1)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率；

(2)若甲、乙两运动员各自射击1次，表示这2次射击中击中9环以上(含9环)的次数，求的分布列及期望．

【答案】（1）0.992；（2）见解析

【解析】

（（1）设甲运动员在3次射击中至少有1次击中9环以上（含9环）为事件，结合次独立重复试验中恰好发生次的概率公式即可求甲运动员在3次射击中至少有1次击中9环以上（含9环）的概率．
（2）根据题意，表示这2次射击中击中9环以上（含9环）的次数的取值是0、1、2，根据互斥事件和相互独立事件同时发生的概率做出结果分布列和期望．

（1）设事件表示“甲运动员射击一次，恰好命中环以上（含环，下同）”，

则.

甲运动员射击次，均未击中环以上的概率为

所以甲运动员射击次，至少次击中环以上的概率

（2）记事件表示“乙运动员射击一次，击中环以上”，

则.

因为表示2次射击击中9环以上的次数，所以的可能取值是0,1,2.

因为

所以的分布列是

X	0	1	2
P	0．05	0．35	0．6

所以

练习册系列答案

相关题目

【题目】抛物线C：y2=4x的焦点为F，斜率为k的直线l与抛物线C交于M，N两点，若线段MN的垂直平分线与x轴交点的横坐标为a（a＞0），n=|MF|+|NF|，则2a﹣n等于（）
A.2
B.3
C.4
D.5

【题目】若定义在R上的函数对任意的、，都有成立，且当时，.

(1)求证：是R上的增函数；

(2)若，解不等式．

【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c，已知向量 =（2a，1）， =（2b﹣c，cosC），且 ∥ ．
（Ⅰ）求角A的大小；
（Ⅱ）若，求b+c的取值范围．

【题目】已知函数f（x）=lnx﹣a（x﹣1），其中a为实数．
（Ⅰ）讨论并求出f（x）的极值；
（Ⅱ）在a＜1时，是否存在m＞1，使得对任意的x∈（1，m）恒有f（x）＞0，并说明理由；
（Ⅲ）确定a的可能取值，使得存在n＞1，对任意的x∈（1，n），恒有|f（x）|＜（x﹣1）2 ．

【题目】已知函数f（x）的定义域为（0，+∞），f′（x）为f（x）的导函数，且满足xf′（x）＞f（x），则不等式（x﹣1）f（x+1）＞f（x2﹣1）的解集是．

【题目】在△ABC中，AB=3，AC=5，cosA= ，点P在平面ABC内，且 =﹣4，则| + +2 |的最大值是．

【题目】如图，某地有三家工厂，分别位于矩形ABCD的顶点A，B以及CD的中点P处，已知AB=20km，CB=10km，为了处理三家工厂的污水，现要在矩形ABCD内(含边界)，且与A，B等距离的一点O处建造一个污水处理厂，并铺设排污管道AO，BO，OP，设排污管道的总长为km．

(I)设，将表示成的函数关系式；

(II)确定污水处理厂的位置，使三条排污管道的总长度最短，并求出最短值．

【题目】为了探究车流量与的浓度是否相关，现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与的数据如表：

时间	星期一	星期二	星期三	星期四	星期五	星期六	星期日
车流量（万辆）	1	2	3	4	5	6	7
的浓度（微克/立方米）	28	30	35	41	49	56	62

（1）求关于的线性回归方程；（提示数据：）

（2）（I）利用（1）所求的回归方程，预测该市车流量为12万辆时的浓度；（II）规定：当一天内的浓度平均值在内，空气质量等级为优；当一天内的浓度平均值在内，空气质量等级为良，为使该市某日空气质量为优或者为良，则应控制当天车流量不超过多少万辆？（结果以万辆为单位，保留整数）参考公式：回归直线的方程是，其中， .

试题分类