题目内容
5.若不等式x2-logmx<0在(0,$\frac{1}{2}$)内恒成立,求实数m的取值范围.分析 在同一坐标系中作y=x2和y=logmx的草图,利用数学结合得出0<m<1,只要x=$\frac{1}{2}$时,y=logm$\frac{1}{2}$≥$\frac{1}{4}$,进而求出a的范围.
解答 解:由x2-logmx<0,得x2<logmx,在同一坐标系中作y=x2和y=logmx的草图,如图所示
要使x2<logmx在(0,$\frac{1}{2}$)内恒成立,只要y=logmx在(0,$\frac{1}{2}$)内的图象在y=x2的上方,于是0<m<1
∵x=$\frac{1}{2}$时,y=$\frac{1}{4}$,
∴只要x=$\frac{1}{2}$时,y=logm$\frac{1}{2}$≥$\frac{1}{4}$
∴$\frac{1}{2}$≤${m}^{\frac{1}{4}}$,即m≥$\frac{1}{16}$
又0<m<1
∴$\frac{1}{16}$≤m<1
即实数m的取值范围为$\frac{1}{16}$≤m<1.
点评 考查了数学结合思想的应用,思路更加直观,易懂.

练习册系列答案
相关题目
15.集合A={x|(x-1)(x+2)<0},集合B={x|lgx≤0},则A∩B=( )
| A. | (0,1) | B. | (0,1] | C. | (-2,1] | D. | (-2,1) |
16.已知球O的直径长为12,当它的内接正四棱锥的体积最大时,该四棱锥的底面边长为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
13.定义在R的函数f(x)满足f(x)f(x+2)=5,f(1)=3,则f(11)=( )
| A. | $\frac{5}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{2}{5}$ |
17.某校企合作工厂机床的生产数量x(百台)与生产成本y(万元)之间有着一定的函数关系,在经济学中称为成本函数,记为C(x).已知这个函数是一元二次函数y=ax2+bx+c(a≠0),且机床的收益函数R(x)=18.5x.经实际测算得到下列数据:
(1)求利润函数L(x):[提示:利润函数L(x)=R(x)-C(x)]
(2)若企业盈利,试求生产数量x的范围.
| 产品数量x | 0 | 3 | 4 | 6 | 7.2 | 10 |
| 生产成本y | 50 | 72.5 | 82 | 104 | 119.2 | 160 |
(2)若企业盈利,试求生产数量x的范围.
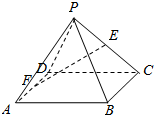 如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.
如图,四棱锥P-ABCD中,ABCD为矩形,面PDC⊥面ABCD,∠DPC=90°,E,F 分别为PC,AD的中点.