题目内容
【题目】已知函数
，
，
.
（1）若函数
在定义域上为单调递增函数，求实数
的取值范围；
（2）设函数，
，
，若存在
使
成立，求实数的取值范围.
【答案】（1）
；（2）
.
【解析】
（1）求出函数
的解析式，由题意得出
对任意的
，利用参变量分离法得出
在恒成立，然后利用基本不等式求出函数
的最大值，可得出实数
的取值范围；
（2）构造函数
，由题意得出
，利用导数求出函数
在区间
上的最大值，然后解不等式即可得出实数的取值范围.
（1）因为
，
，
所以
，所以
，
据题意，得对
成立，
所以只需
对成立，
所以只需在恒成立，
又当时，
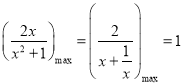，所以
，
即所求实数的取值范围是；
（2）据题意，存在
使
成立，
引入
，则
，
又因为
，
，所以
恒成立，
所以函数在上是增函数，所以当时，
，
所以
，所以
，所以的取值范围是.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】2018年上海国际青少年足球邀请赛将在6月下旬举行.一体育机构对某高中一年级750名男生，600名女生采用分层抽样的方法抽取45名学生对足球进行兴趣调查，统计数据如下所示：
表1：男生
结果 | 有兴趣 | 无所谓 | 无兴趣 |
人数 |
| 2 | 3 |
表2：女生
结果 | 有兴趣 | 无所谓 | 无兴趣 |
人数 | 12 |
| 2 |
（1）求
，
的值；
（2）运用独立性检验的思想方法分析：请你填写
列联表，并判断是否在犯错误的概率不超过
的前提下认为非“有兴趣”与性别有关系？
男生 | 女生 | 总计 | |
有兴趣 | |||
非有兴趣 | |||
总计 |
（3）从45人所有无兴趣的学生中随机选取2人，求所选2人中至少有一个女生的概率.
附：
，
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
