题目内容
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,点
,点![]() ,
,![]() 在该抛物线上且位于
在该抛物线上且位于![]() 轴的两侧,
轴的两侧,![]() .
.
(Ⅰ)证明:直线![]() 过定点
过定点![]() ;
;
(Ⅱ)以![]() ,
,![]() 为切点作
为切点作![]() 的切线,设两切线的交点为
的切线,设两切线的交点为![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)证明见解析;(Ⅱ)2.
【解析】
(Ⅰ)先求出抛物线的方程,然后设直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() (
(![]() ,
,![]() ),联立直线和抛物线的方程可得
),联立直线和抛物线的方程可得![]() ,由韦达定理可得
,由韦达定理可得![]() 的值,再根据
的值,再根据![]() ,可得出b的值,进而可得出直线恒过定点;
,可得出b的值,进而可得出直线恒过定点;
(Ⅱ)以![]() 为切点的切线方程为
为切点的切线方程为![]() ,以
,以![]() 为切点的切线方程为
为切点的切线方程为![]() ,联立
,联立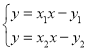 ,解得
,解得![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,所以两切线交点
,所以两切线交点![]() 的轨迹方程为
的轨迹方程为![]() ,进而可得出
,进而可得出![]() 的最小值.
的最小值.
(Ⅰ)根据题意,![]() ,所以
,所以![]() .
.
故抛物线![]() .
.
由题意设直线![]() 的方程为
的方程为![]() .
.
由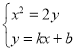 ,消去
,消去![]() 整理得
整理得![]() .
.
显然![]() .
.
设![]() ,
,![]() (
(![]() ,
,![]() ),则
),则![]() ,
,
所以![]() .
.
由题意得![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
所以直线![]() 的方程为
的方程为![]() ,故直线
,故直线![]() 过定点
过定点![]() ;
;
(Ⅱ)因为![]() ,所以
,所以![]() ,
,![]() ,
,
故以![]() 为切点的切线方程为
为切点的切线方程为![]() ,即
,即![]() ,
,
以![]() 为切点的切线方程为
为切点的切线方程为![]() ,即
,即![]()
联立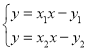 ,解得
,解得![]() .
.
又因为![]() ,
,
所以两切线交点![]() 的轨迹方程为
的轨迹方程为![]() .
.
因为圆心到直线![]() 的距离为3,
的距离为3,
所以圆上一点到直线![]() 的最小距离为
的最小距离为![]() ,
,
故![]() 的最小值为2.
的最小值为2.

练习册系列答案
相关题目
【题目】某中学高三(3)班全班50人参加了高考前的数学模拟测试,每名学生要在规定的2个小时内做一套高三模拟卷,现抽取10位学生的成绩,分为甲,乙两组,其分数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 64 | 72 | 86 | 98 | 120 |
乙组 | 60 | 76 | 90 | 92 | 122 |
(Ⅰ)分别求出甲,乙两组学生考试所得分数的平均数及方差,并由此分析两组学生的成绩水平;
(Ⅱ)试估计全班有多少人及格(90分及以上为及格);
(Ⅲ)从该班级甲,乙两组中各随机抽取1名学生,对其考试成绩进行抽查,求两人考试分数之和大于等于180的概率.