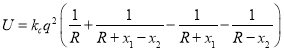题目内容
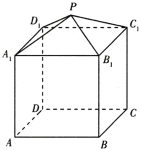
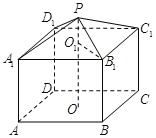
【题目】如图是一个由正四棱锥
和正四棱柱
构成的组合体，正四棱锥的侧棱长为6，
为正四棱锥高的4倍.当该组合体的体积最大时，点
到正四棱柱外接球表面的最小距离是（ ）
A.
B.
C.
D.
【答案】B
【解析】
设正四棱锥的高为
，
，由条件可得
，然后该组合体的体积为
，然后利用导数求出当
时体积取得最大值，此时
，然后算出正四棱柱
外接球的半径，然后点
到正四棱柱外接球表面的最小距离为点到球心的距离减去半径，即可得到答案.
设正四棱锥的高为，，
由正四棱锥的侧棱长为6可得，
该组合体的体积为
，
令
，则
，
所以可得
在
上单调递增，在
上单调递减，
所以当时取得最大值，即该组合体的体积最大,
此时,
所以正四棱柱的外接球半径为:
,
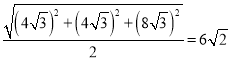点到正四棱柱外接球表面的最小距离为点到球心的距离减去半径，
即
,
故选：B
练习册系列答案
阅读快车系列答案
相关题目
