题目内容
(本题满分15分)已知各项均不相等的等差数列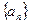 的前四项和
的前四项和 ,且
,且 成等比.
成等比.
(Ⅰ)求数列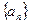 的通项公式;
的通项公式;
(Ⅱ)设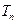 为数列
为数列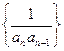 的前n项和,若
的前n项和,若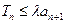 对一切
对一切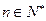 恒成立,求实数
恒成立,求实数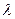 的最小值.
的最小值.
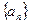 的前四项和
的前四项和 ,且
,且 成等比.
成等比.(Ⅰ)求数列
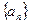 的通项公式;
的通项公式;(Ⅱ)设
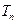 为数列
为数列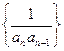 的前n项和,若
的前n项和,若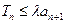 对一切
对一切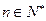 恒成立,求实数
恒成立,求实数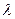 的最小值.
的最小值.解:(Ⅰ)设公差为d,则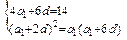 ,
,
解得d=1或d=0(舍去),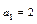 -----------------------------------------------------------3分
-----------------------------------------------------------3分
所以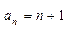 ----------------------------------------------------3分
----------------------------------------------------3分
(Ⅱ)因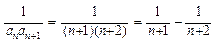 ----------------------------2分
----------------------------2分
故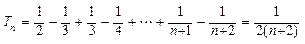 ----------------------- --2分
----------------------- --2分
又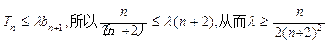
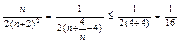 ,-------------------------------- 3分
,-------------------------------- 3分
因此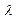 的最小值为
的最小值为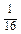 ----------------------1分
----------------------1分
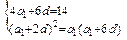 ,
,解得d=1或d=0(舍去),
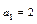 -----------------------------------------------------------3分
-----------------------------------------------------------3分所以
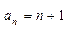 ----------------------------------------------------3分
----------------------------------------------------3分(Ⅱ)因
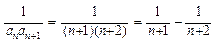 ----------------------------2分
----------------------------2分故
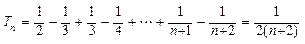 ----------------------- --2分
----------------------- --2分又
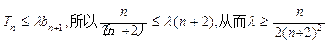
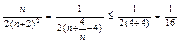 ,-------------------------------- 3分
,-------------------------------- 3分因此
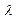 的最小值为
的最小值为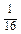 ----------------------1分
----------------------1分略

练习册系列答案
相关题目
 的前
的前 项和满足
项和满足 ,下列结论正确的是( )
,下列结论正确的是( ) 是
是 中最大值
中最大值

 }中,已知a1=
}中,已知a1= ,a2+a5=4,
,a2+a5=4, =242,求首项a1和项数n.
=242,求首项a1和项数n.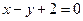 上。
上。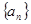 是等差数列,
是等差数列,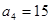 ,
,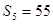 ,则过点
,则过点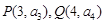 的直线的斜
的直线的斜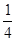
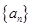 中,已知
中,已知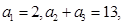 则
则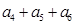 等于 ( )
等于 ( )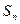 是等差数列
是等差数列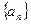 的前
的前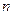 项和,若
项和,若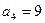 ,
,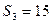 ,则数列
,则数列