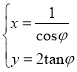题目内容
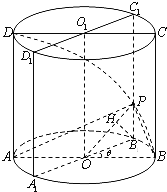
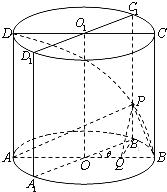
【题目】已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ<π)后,边B1C1与曲线Γ相交于点P.
(1)求曲线Γ长度;
(2)当![]() 时,求点C1到平面APB的距离;
时,求点C1到平面APB的距离;
(3)是否存在θ,使得二面角D﹣AB﹣P的大小为![]() ?若存在,求出线段BP的长度;若不存在,请说明理由.
?若存在,求出线段BP的长度;若不存在,请说明理由.
【答案】(1)![]() π;(2)
π;(2)![]() ;(3)不存在,理由见解析
;(3)不存在,理由见解析
【解析】
(1)将圆柱一半展开后底面的半个圆周变成长方形的边BA,曲线Γ就是对角线BD,从而可求曲线Γ长度;
(2)当θ![]() 时,点B1恰好为AB的中点,所以P为B1C1中点,故点C1到平面APB的距离与点B1到平面APB的距离相等.
时,点B1恰好为AB的中点,所以P为B1C1中点,故点C1到平面APB的距离与点B1到平面APB的距离相等.
(3)由于二面角D﹣AB﹣B1为直二面角,故只要考查二面角P﹣AB﹣B1是否为![]() 即可.
即可.
解:(1)将圆柱一半展开后底面的半个圆周变成长方形的边BA,曲线Γ就是对角线BD.
由于AB=πr=π,AD=π,所以这实际上是一个正方形.
所以曲线Γ的长度为BD![]() π.
π.
(2)当θ![]() 时,点B1恰好为AB的中点,所以P为B1C1中点,
时,点B1恰好为AB的中点,所以P为B1C1中点,
故点C1到平面APB的距离与点B1到平面APB的距离相等.
连接AP、BP,OP.
由AB⊥B1P且AB⊥A1B1知:AB⊥平面A1B1P,从而平面A1B1P⊥平面APB.
作B1H⊥OP于H,则B1H⊥平面APB,所以B1H即为点B1到平面APB的距离.
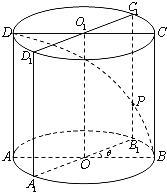
在Rt△OB1P中,![]()
由(1)可知,圆柱的一半展开后得到一个正方形,所以![]()
所以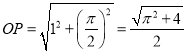 .
.
于是: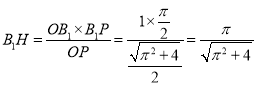 .
.
所以,点C1到平面APB的距离为![]() .
.
(3)由于二面角D﹣AB﹣B1为直二面角,故只要考查二面角P﹣AB﹣B1是否为![]() 即可.
即可.
过B1作B1Q⊥AB于Q,连接PQ.
由于B1Q⊥AB,B1P⊥AB,所以AB⊥平面B1PQ,所以AB⊥PQ.
于是∠PQB1即为二面角P﹣AB﹣B1的平面角.
在Rt△PB1Q中,![]() .
.
由(2)有![]()
若![]() ,则需B1P=B1Q,即sinθ=θ.
,则需B1P=B1Q,即sinθ=θ.
令f(x)=sinx﹣x(0<x<π),则f′(x)=cosx﹣1<0,
故f(x)在(0,π)单调递减.
所以f(x)<f(0)=0,即sinx<x在(0,π)上恒成立.
故不存在θ∈(0,π),使sinθ=θ.
也就是说,不存在θ∈(0,π),使二面角D﹣AB﹣P为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案