题目内容
7.若关于x的方程kx+1=lnx有两个不同实数解,则实数k的取值范围是(0,$\frac{1}{{e}^{2}}$).分析 作f(x)=kx+1与g(x)=lnx的图象,利用数形结合的思想求解即可.
解答 解:令f(x)=kx+1,g(x)=lnx,
作f(x)=kx+1与g(x)=lnx的图象如下,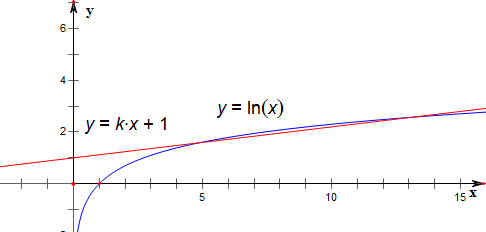
设直线f(x)=kx+1与g(x)=lnx相切于点(a,b);
则$\left\{\begin{array}{l}{k=\frac{1}{a}}\\{b=lna}\\{b=ka+1}\end{array}\right.$,
解得,k=$\frac{1}{{e}^{2}}$;
且对数函数g(x)=lnx的增长速度越来越慢,
结合函数图象可知,k>0;
故实数k的取值范围是(0,$\frac{1}{{e}^{2}}$).
故答案为:(0,$\frac{1}{{e}^{2}}$).
点评 本题考查了导数的几何意义的应用及数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
2.某同学为了解秋冬季节用电量(y度)与气温(x℃)的关系,由下表数据计算出回归直线方程为y=-2x+60,则表中a的值为( )
| 气温 | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | a | 64 |
| A. | 40 | B. | 39 | C. | 38 | D. | 37 |
19.已知两直线2x-y+1=0与3x+ay=0平行,则a=( )
| A. | $-\frac{3}{2}$ | B. | -3 | C. | -4 | D. | -5 |
