题目内容
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点F的距离为5.
到其焦点F的距离为5.
(1)求抛物线C的方程;
(2)设直线l与抛物线C交于A、B两点,O为坐标原点,若![]() ,求证:直线l必过一定点,并求出该定点的坐标;
,求证:直线l必过一定点,并求出该定点的坐标;
(3)过点![]() 的直线m与抛物线C交于不同的两点M、N,若
的直线m与抛物线C交于不同的两点M、N,若![]() ,求直线m的斜率的取值范围.
,求直线m的斜率的取值范围.
【答案】(1)![]() (2)直线l过定点
(2)直线l过定点![]() ,证明见解析(3)
,证明见解析(3)![]()
【解析】
(1)解法1:根据抛物线的定义列方程![]() ,求得p的值,写出抛物线方程;
,求得p的值,写出抛物线方程;
解法2:将![]() 代入
代入![]() ,再由点T到其焦点F的距离,
,再由点T到其焦点F的距离,
列出方程组求得p的值,再写出抛物线方程;
(2)可直线l的方程为![]() ,与抛物线方程联立,消去y,
,与抛物线方程联立,消去y,
利用根与系数的关系计算![]() ,从而证明直线l过定点
,从而证明直线l过定点![]() ;
;
(3)依题意设直线m的方程为![]() ,与抛物线方程联立,消去y,
,与抛物线方程联立,消去y,
利用根与系数的关系计算![]() ,由
,由![]() 得k的取值范围.
得k的取值范围.
解:(1)解法1:由题意,根据抛物线的定义,有![]() ,解得
,解得![]() ,
,
所以抛物线C的方程为![]() ;
;
解法2:将![]() 代入
代入![]() 得,
得,![]() ,
,
又点![]() 到其焦点F的距离为5,焦点坐标为
到其焦点F的距离为5,焦点坐标为![]() ,所以
,所以![]() ,
,
将![]() 代入整理得
代入整理得![]() ,解得
,解得![]() ,
,
故抛物线C的方程为![]() ;
;
(2)依题意,直线l的斜率存在,设l的方程为![]() ,
,
由![]() 得
得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]()
![]() ,
,
令![]() ,得
,得![]() ,所以直线l过定点
,所以直线l过定点![]() .
.
(3)依题意,直线m的斜率k存在且![]() ,设m的方程为
,设m的方程为![]() ,
,
由![]() 消去y,得
消去y,得![]() ,
,
由![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,
所以![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,解得
,解得![]() ;
;
所以,直线m的斜率的取值范围是![]() .
.

【题目】研学旅行是研究性学习和旅行体验相结合的校外教育活动,继承和发展了我国传统游学、“读万卷书,行万里路”的教育理念和人文精神,成为素质教育的新内容和新方式,提升中小学生的自理能力、创新精神和实战能力,是综合实战育人的有效途径,为了了解某校高二年级600名学生在一次研学旅行活动中的武术表演情况,研究人员在该校高二学生中随机抽取了10名学生的武术表演成绩进行统计,统计结果如图所示(满分100分),已知这10名学生或武术表演的平均成绩为85分.
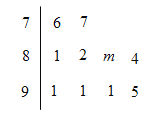
(1)求m的值;
(2)为了研究高二男、女生的武术表演情况,现对该校高二所有学生的武术表演成绩进行分类统计,得到的数据如下表所示:
男生 | 女生 | 合计 | |
武术表演成绩超过80分 | 150 | ||
武术表演成绩不超过80分 | 100 | ||
合计 |
已知随机抽取这600名学生中的一名学生,抽到武术表演成绩超过80分的学生概率是![]() ,根据已知条件完成上面
,根据已知条件完成上面![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为武术表演成绩超过80分与性别具有相关性.
的把握认为武术表演成绩超过80分与性别具有相关性.
参考公式: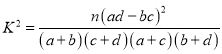 ,其中
,其中![]() .
.
临界值表:
P( | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某商场周年庆,准备提供一笔资金,对消费满一定金额的顾客以参与活动的方式进行奖励.顾客从一个装有大小相同的2个红球和4个黄球的袋中按指定规则取出2个球,根据取到的红球数确定奖励金额,具体金额设置如下表:
取到的红球数 | 0 | 1 | 2 |
奖励(单位:元) | 5 | 10 | 50 |
现有两种取球规则的方案:
方案一:一次性随机取出2个球;
方案二:依次有放回取出2个球.
(Ⅰ)比较两种方案下,一次抽奖获得50元奖金概率的大小;
(Ⅱ)为使得尽可能多的人参与活动,作为公司的负责,你会选择哪种方案?请说明理由.