题目内容
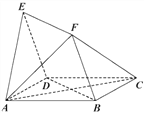
【题目】如图,四边形![]() 与
与![]() 均为菱形,
均为菱形,![]() ,且
,且![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若![]() 为线段
为线段![]() 上的一点,且满足直线
上的一点,且满足直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)二面角![]() 的余弦值为
的余弦值为![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)由菱形的性质可得![]() ,由等腰三角形的性质可得
,由等腰三角形的性质可得![]() ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得![]() 平面
平面![]() ;(2)先证明
;(2)先证明![]() 为等边三角形,可得
为等边三角形,可得![]() ,于是可以
,于是可以![]() 为坐标轴建立坐标系,利用向量垂直数量积为零,列方程组求出平面
为坐标轴建立坐标系,利用向量垂直数量积为零,列方程组求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,利用空间向量夹角余弦公式可得结果;(3)设
的法向量,利用空间向量夹角余弦公式可得结果;(3)设![]() 由直线
由直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,利用空间向量夹角余弦公式列方程求得
,利用空间向量夹角余弦公式列方程求得![]() ,从而可得结果.
,从而可得结果.
详解:(1)设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,
∵四边形![]() 为菱形,∴
为菱形,∴![]() ,
,
且![]() 为
为![]() 中点,
中点,
∵![]() ,∴
,∴![]() ,
,
又![]() ,
,![]()
∴![]() 平面
平面![]() .
.
(2)连接![]() ,∵四边形
,∵四边形![]() 为菱形,且
为菱形,且![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∵![]() 为
为![]() 中点,∴
中点,∴![]() ,又
,又![]() ,
,
![]() ∴
∴![]() 平面
平面![]() .∵
.∵![]() 两两垂直,∴建立空间直角坐标系
两两垂直,∴建立空间直角坐标系![]() ,如图所示,
,如图所示,
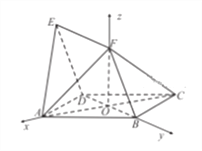
设![]() ,∵四边形
,∵四边形![]() 为菱形,
为菱形, ![]() ,∴
,∴![]() .
.
∵![]() 为等边三角形,∴
为等边三角形,∴![]() .
.
∴![]() ,
,
∴![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则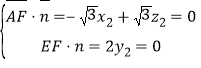
令![]() ,得
,得![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则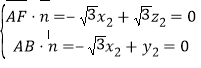 ,
,
令![]() ,得
,得![]()
所以 ![]()
又因为二面角![]() 为钝角,
为钝角,
所以二面角![]() 的余弦值为
的余弦值为![]()
(3)设![]()
![]()
![]()
所以 ![]()
化简得![]()
解得:![]()
所以![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】近年来,共享单车在我国各城市迅猛发展,为人们的出行提供了便利,但也给城市的交通管理带来了一些困难,为掌握共享单车在![]() 省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的
省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的![]() 指标
指标![]() 和
和![]() 指标
指标![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并说明
,并说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的线性相关关系,否则认为没有较强的线性相关关系).
具有较强的线性相关关系,否则认为没有较强的线性相关关系).
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标为7时,
指标为7时,![]() 指标的估计值.
指标的估计值.
(3)若某城市的共享单车![]() 指标
指标![]() 在区间
在区间![]() 的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至
的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至![]() 指标
指标![]() 在区间
在区间![]() 内现已知
内现已知![]() 省某城市共享单车的
省某城市共享单车的![]() 指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为
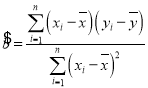 ,,
,,![]() 相关系数
相关系数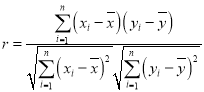
参考数据: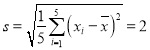 ,
,![]() ,
,![]() .
.
【题目】为了解使用手机是否对学生的学习有影响,某校随机抽取100名学生,对学习成绩和使用手机情况进行了调查,统计数据如表所示(不完整):
使用手机 | 不使用手机 | 总计 | |
学习成绩优秀 | 10 | 40 | |
学习成绩一般 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有99.9%的把握认为学生的学习成绩与使用手机有关;
(2)现从上表中不使用手机的学生中按学习成绩是否优秀分层抽样选出6人,再从这6人中随机抽取3人,求其中学习成绩优秀的学生恰有2人的概率.
参考公式: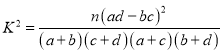 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |