题目内容
【题目】同时具有性质:“①最小正周期是π;②图象关于直线 ![]() 对称;③在
对称;③在 ![]() 上是增函数.”的一个函数为( )
上是增函数.”的一个函数为( )
A.![]()
B.![]() ??
??
C.![]()
D.![]()
【答案】D
【解析】解:由于y=sin( ![]() +
+ ![]() )的最小正周期为
)的最小正周期为 ![]() =4π,不满足①,故排除A. 由于y=cos(
=4π,不满足①,故排除A. 由于y=cos( ![]() ﹣
﹣ ![]() )的最小正周期为
)的最小正周期为 ![]() =4π,不满足①,故排除B.
=4π,不满足①,故排除B.
由于y=cos(2x+ ![]() ),在
),在 ![]() 上,2x+
上,2x+ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
故y=cos(2x+ ![]() )在
)在 ![]() 上没有单调性,故排除C.
上没有单调性,故排除C.
对于y=sin(2x﹣ ![]() )的最小正周期为
)的最小正周期为 ![]() =π;
=π;
当 ![]() 时,函数取得最大值为1,故图象关于直线
时,函数取得最大值为1,故图象关于直线 ![]() 对称;
对称;
在 ![]() 上,2x﹣
上,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],故y=sin(2x﹣
],故y=sin(2x﹣ ![]() )在
)在 ![]() 上是增函数,
上是增函数,
故D满足题中的三个条件,
故选:D.
【考点精析】根据题目的已知条件,利用正弦函数的单调性和正弦函数的对称性的相关知识可以得到问题的答案,需要掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;正弦函数的对称性:对称中心
上是减函数;正弦函数的对称性:对称中心![]() ;对称轴
;对称轴![]() .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位: ![]() ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示一天内抽取的16个零件中其尺寸在
表示一天内抽取的16个零件中其尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及
及![]() 的数学期望;
的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得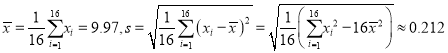 ,其中
,其中![]() 为
为
抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() .
.



