[题目]如图,在直三棱柱ABCA1B1C1中,D是BC的中点．(1)求证:A1B∥平面ADC1;(2)若AB⊥AC,AB＝AC＝1,AA1＝2,求几何体ABD-A1B1C1的体积．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图,在直三棱柱ABCA1B1C1中,D是BC的中点．

(1)求证:A1B∥平面ADC1;

(2)若AB⊥AC,AB＝AC＝1,AA1＝2,求几何体ABD-A1B1C1的体积．

【答案】（1）详见解析（2）

【解析】试题分析：（1）连接，与交于点，连接，然后证明∥即可；（2）用三棱柱的体积减去三棱锥的体积即可.

试题解析：(1)证明:连接A1C,与AC1交于点O,连接DO,

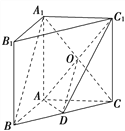
由直三棱柱性质可知，侧棱垂直于底面，侧面为矩形

∴O为AC1中点，则A1B∥OD.

又∵OD平面ADC1，A1B平面ADC1,

∴A1B∥平面ADC1.

(2)由于是直棱柱，所以侧棱长就是几何体的高,

又∵AB⊥AC

∴底面为直角三角形,

∴＝Sh＝×1×1×2＝1， -ACD＝Sh＝×××1×1×2=

∴＝--ACD＝.

练习册系列答案

相关题目

【题目】在平行四边形ABCD中，A(1，1)，＝(6，0)，点M是线段AB的中点，线段CM与BD交于点P．(1) 若＝(3，5)，求点C的坐标；(2) 当||＝||时，求点P的轨迹．

【题目】甲、乙两同学利用暑假到某县进行社会实践，对该县的养鸡场连续六年来的规模进行调查研究，得到如下两个不同的信息图：

（A）图表明：从第1年平均每个养鸡场出产1万只鸡上升到第6年平均每个养鸡场出产2万只鸡：

（B）图表明：由第1年养鸡场个数30个减少到第6年的10个.

请你根据提供的信息解答下列问题：

（1）第二年的养鸡场的个数及全县出产鸡的总只数各是多少？

（2）哪一年的规模最大？为什么？

【题目】某厂生产某种产品的年固定成本为250万元，每生产x千件，需另投入成本C（x），当年产量不足80千件时，C（x）= x2+10x（万元）；当年产量不小于80千件时C（x）=51x+ ﹣1450（万元），通过市场分析，若每件售价为500元时，该厂本年内生产该商品能全部销售完．
（1）写出年利润L（万元）关于年产量x（千件）的函数解析式；
（2）年产量为多少千件时，该厂在这一商品的生产中所获的利润最大？

【题目】已知函数f（x）满足：对任意x，y∈R，都有f（x+y）=f（x）f（y）﹣f（x）﹣f（y）+2成立，且x＞0时，f（x）＞2，
（1）求f（0）的值，并证明：当x＜0时，1＜f（x）＜2．
（2）判断f（x）的单调性并加以证明．
（3）若函数g（x）=|f（x）﹣k|在（﹣∞，0）上递减，求实数k的取值范围．