题目内容
(本小题满分14分)
.如图,ABCD是梯形,AB//CD,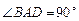 ,PA⊥面ABCD, 且AB=1,AD=1,CD=2,PA=3,E为PD的中点
,PA⊥面ABCD, 且AB=1,AD=1,CD=2,PA=3,E为PD的中点
(Ⅰ)求证:AE//面PBC.
(Ⅱ)求直线AC与PB所成角的余弦值;(Ⅲ)在面PAB内能否找一点N,使NE⊥面PAC. 若存在,找出并证明;若不存在,请说明理由。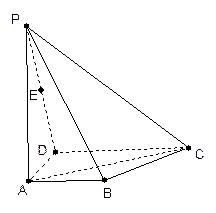
|
|
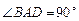 ,PA⊥面ABCD, 且AB=1,AD=1,CD=2,PA=3,E为PD的中点
,PA⊥面ABCD, 且AB=1,AD=1,CD=2,PA=3,E为PD的中点(Ⅰ)求证:AE//面PBC.
|


|
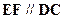 且
且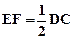
所以EF//AB,且EF=AB,所以ABFE为平行四边形 …2分
所以AE//BF, 因为AE
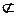 面PBC,所以AE//面PBC …4分
面PBC,所以AE//面PBC …4分(Ⅱ)建立如图所示的空间直角坐标系,
则 A、B、C、D、P、E的坐标分别为A(0,0,0),
B(1,0,0),C(2,1,0),D(0,1,0),
(0,0,3),E(0,
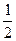 ,
,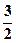 )…5分
)…5分从而
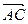 =(2,1,0),
=(2,1,0),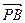 =(1,0,
=(1,0, )
)设
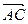 与
与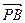 的夹角为
的夹角为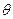 ,则
,则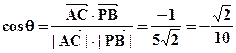 , …7分
, …7分∴AC与PB所成角的余弦值为
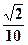 …8分
…8分(Ⅲ)法1:由于N点在面PAB内,故可设N点坐标为(x,0,z),
则
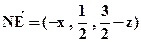 由NE⊥面PAC可得:
由NE⊥面PAC可得: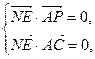 …10分
…10分即
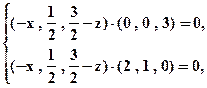
化简得
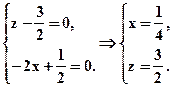 即N点的坐标为(
即N点的坐标为(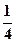 ,0,
,0,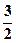 )
) 所以在面PAB内存在点N(
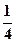 ,0,
,0,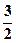 ),使NE⊥面PAC. …14分
),使NE⊥面PAC. …14分(Ⅲ)法2:在面ABCD内过D作AC的垂线交AB于G,连PG,
设N为PG的中点,连NE,则NE//DG, …10分
∵DG⊥AC,DG⊥PA,∴DG⊥面PAC 从而NE⊥面PAC …14分
略

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 ,则该几何体的俯视图可以是( )
,则该几何体的俯视图可以是( ) 
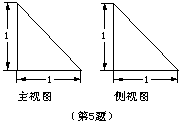
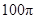 B.
B.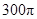 C.
C.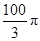 D.
D.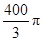
 中,二面角
中,二面角 的平面角等于 ( )
的平面角等于 ( ) B.
B. C .
C . D
D 

 _____________
_____________ 
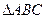 的三个顶点距离均为1cm的平面共有 .
的三个顶点距离均为1cm的平面共有 . 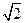 ,
,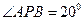 ,点E、F分别在侧棱PB、PC上,则
,点E、F分别在侧棱PB、PC上,则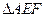 周长的最小值为 .
周长的最小值为 .