题目内容
已知函数f(x)=ln(x+1)+ax2-x,a∈R.
(1)当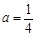 时,求函数y=f(x)的极值;
时,求函数y=f(x)的极值;
(2)是否存在实数b∈(0,1),使得当x∈(-1,b]时,函数f(x)的最大值为f(b)?若存在,求实数a的取值范围,若不存在,请说明理由.
(1)当
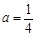 时,求函数y=f(x)的极值;
时,求函数y=f(x)的极值;(2)是否存在实数b∈(0,1),使得当x∈(-1,b]时,函数f(x)的最大值为f(b)?若存在,求实数a的取值范围,若不存在,请说明理由.
(1)在x=1处取到极小值为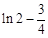 ,在x=0处取到极大值为0;(2)
,在x=0处取到极大值为0;(2)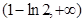 .
.
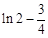 ,在x=0处取到极大值为0;(2)
,在x=0处取到极大值为0;(2)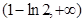 .
.试题分析:(1)将
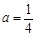 代入函数f(x)解析式,求出函数f(x)的导函数,令导函数等于零,求出其根;然后列出x的取值范围与
代入函数f(x)解析式,求出函数f(x)的导函数,令导函数等于零,求出其根;然后列出x的取值范围与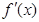 的符号及f(x)的单调性情况表,从表就可得到函数f(x)的极值;(2)由题意首先求得:
的符号及f(x)的单调性情况表,从表就可得到函数f(x)的极值;(2)由题意首先求得: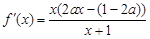 ,故应按
,故应按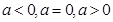 分类讨论:当a≤0时,易知函数f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,从而当b∈(0,1)时f(b)<f(0),所以不存在实数b∈(0,1),符合题意;当a>0时,令
分类讨论:当a≤0时,易知函数f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,从而当b∈(0,1)时f(b)<f(0),所以不存在实数b∈(0,1),符合题意;当a>0时,令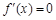 有x=0或
有x=0或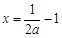 ,又要按根
,又要按根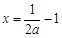 大于零,小于零和等于零分类讨论;对各种情况求函数f(x)x∈(-1,b]的最大值,使其最大值恰为f(b),分别求得a的取值范围,然而将所得范围求并即得所求的范围;若求得的a的取值范围为空则不存在,否则存在.
大于零,小于零和等于零分类讨论;对各种情况求函数f(x)x∈(-1,b]的最大值,使其最大值恰为f(b),分别求得a的取值范围,然而将所得范围求并即得所求的范围;若求得的a的取值范围为空则不存在,否则存在.试题解析:(1)当
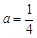 时,
时,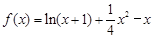 ,
,则
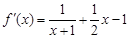 ,化简得
,化简得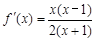 (x>-1) 2分
(x>-1) 2分 列表如下:
| x | (-1,0) | 0 | (0,1) | 1 | (1,+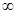 ) ) |
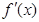 | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
∴函数f(x)在(-1,0),(1,+∞)上单调递增,在(0,1)上单调递减,且f(0)=0,
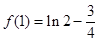 , 4分
, 4分∴函数y=f(x)在x=1处取到极小值为
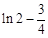 ,
,在x=0处取到极大值为0; 5分
(2)由题意
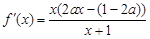
(1)当a≤0时,函数f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
此时,不存在实数b∈(0,1),使得当x∈(-1,b]时,函数f(x)的最大值为f(b); 7分
(2)当a>0时,令
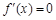 有x=0或
有x=0或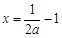 ,
,(ⅰ)当
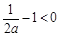 即
即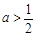 时,函数f(x)在
时,函数f(x)在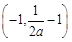 和(0,+∞)上单调递增,在
和(0,+∞)上单调递增,在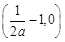 上单调递减,要存在实数b∈(0,1),使得当x∈(-1,b]时,函数f(x)的最大值为f(b),则
上单调递减,要存在实数b∈(0,1),使得当x∈(-1,b]时,函数f(x)的最大值为f(b),则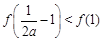 ,代入化简得
,代入化简得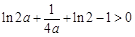 (1)
(1)令
 ,因
,因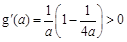 恒成立,
恒成立,故恒有
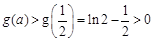 ,∴
,∴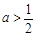 时,(1)式恒成立; 10分
时,(1)式恒成立; 10分(ⅱ)当
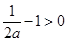 即
即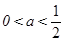 时,函数f(x)在
时,函数f(x)在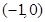 和
和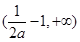 上单调递增,在
上单调递增,在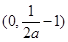 上单调递减,此时由题,只需
上单调递减,此时由题,只需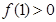 ,解得
,解得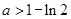 ,又
,又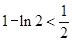 ,
,∴此时实数a的取值范围是
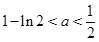 ; 12分
; 12分(ⅲ)当
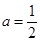 时,函数f(x)在
时,函数f(x)在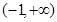 上单调递增,
上单调递增,显然符合题意; 13分
综上,实数a的取值范围是
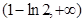 . 14分
. 14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
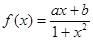 是定义在
是定义在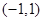 上的奇函数,且
上的奇函数,且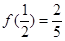 .
.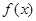 的解析式;
的解析式;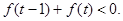 .
.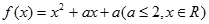 ,
,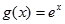 ,
,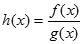
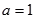 时,求
时,求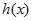 的单调区间
的单调区间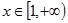 上是递减的,求实数
上是递减的,求实数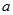 的取值范围;
的取值范围; 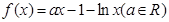 .
.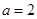 时,求函数
时,求函数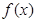 的单调区间;
的单调区间;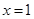 处取得极值,对
处取得极值,对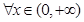 ,
,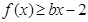 恒成立,求实数
恒成立,求实数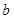 的取值范围;
的取值范围;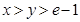 时,求证:
时,求证: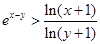 .
.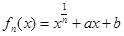
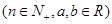 .
.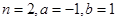 时,求函数
时,求函数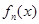 的极值;
的极值;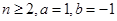 ,证明:
,证明: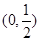 内存在唯一的零点;
内存在唯一的零点;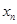 是
是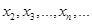 的增减性.
的增减性. 在R上开导,且
在R上开导,且 ,若
,若 ,则不等式
,则不等式 的解集为( )
的解集为( )


