题目内容
已知函数f(x)=xlnx,g(x)=-x2+ax-3,其中a为实数.
(1)设t>0为常数,求函数f(x)在区间[t,t+2]上的最小值;
(2)若对一切x∈(0,+∞),不等式2f(x)≥g(x)恒成立,求实数a的取值范围.
(1)设t>0为常数,求函数f(x)在区间[t,t+2]上的最小值;
(2)若对一切x∈(0,+∞),不等式2f(x)≥g(x)恒成立,求实数a的取值范围.
(1)f'(x)=lnx+1,
当x∈(0,
),f′(x)<0,f(x)单调递减,当x∈(
,+∞),f′(x)>0,f(x)单调递增
①0<t<t+2<
,没有最小值;
②0<t<
<t+2,即0<t<
时,f(x)min=f(
)=-
;
③
≤t<t+2,即t≥
时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt;(5分)
所以f(x)min=
(2)由已知,
2xlnx≥-x2+ax-3,则a≤2lnx+x+
,
设h(x)=2lnx+x+
(x>0),则h′(x)=
,
①x∈(0,1),h'(x)<0,h(x)单调递减,
②x∈(1,+∞),h'(x)>0,h(x)单调递增,
所以h(x)min=h(1)=4,对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
所以a≤h(x)min=4;
当x∈(0,
| 1 |
| e |
| 1 |
| e |
①0<t<t+2<
| 1 |
| e |
②0<t<
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
③
| 1 |
| e |
| 1 |
| e |
所以f(x)min=
|
(2)由已知,
2xlnx≥-x2+ax-3,则a≤2lnx+x+
| 3 |
| x |
设h(x)=2lnx+x+
| 3 |
| x |
| (x+3)(x-1) |
| x2 |
①x∈(0,1),h'(x)<0,h(x)单调递减,
②x∈(1,+∞),h'(x)>0,h(x)单调递增,
所以h(x)min=h(1)=4,对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
所以a≤h(x)min=4;

练习册系列答案
相关题目
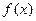 是定义在
是定义在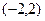 上的减函数,若
上的减函数,若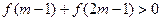 ,求实数
,求实数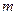 的取值范围。
的取值范围。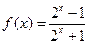 ,(Ⅰ)证明函数
,(Ⅰ)证明函数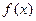 是R上的增函数;
是R上的增函数;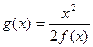 .判定函数
.判定函数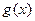 的奇偶性,并证明
的奇偶性,并证明