题目内容
(2013•天津)已知函数f(x)=x2lnx.
(1)求函数f(x)的单调区间;
(2)证明:对任意的t>0,存在唯一的s,使t=f(s).
(3)设(2)中所确定的s关于t的函数为s=g(t),证明:当t>e2时,有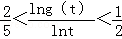 .
.
(1)求函数f(x)的单调区间;
(2)证明:对任意的t>0,存在唯一的s,使t=f(s).
(3)设(2)中所确定的s关于t的函数为s=g(t),证明:当t>e2时,有
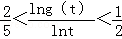 .
.(1)所以函数f(x)的单调递减区间为(0,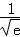 ),单调递增区间为(
),单调递增区间为( 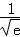 ,+∞)
,+∞)
(2)见解析 (3)见解析
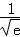 ),单调递增区间为(
),单调递增区间为( 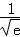 ,+∞)
,+∞)(2)见解析 (3)见解析
(1)由题意可知函数的定义域为(0,+∞),
求导数可得f′(x)=2xlnx+x2• =2xlnx+x=x(2lnx+1),
=2xlnx+x=x(2lnx+1),
令f′(x)=0,可解得x=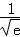 ,
,
当x变化时,f′(x),f(x)的变化情况如下表:
所以函数f(x)的单调递减区间为(0,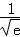 ),单调递增区间为(
),单调递增区间为( 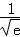 ,+∞)
,+∞)
(2)证明:当0<x≤1时,f(x)≤0,设t>0,令h(x)=f(x)﹣t,x∈[1,+∞),
由(1)可知,h(x)在区间(1,+∞)单调递增,h(1)=﹣t<0,h(et)=e2tlnet﹣t=t(e2t﹣1)>0,
故存在唯一的s∈(1,+∞),使得t=f(s)成立;
(3)证明:因为s=g(t),由(2)知,t=f(s),且s>1,
从而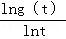 =
=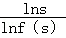 =
=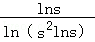 =
=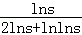 =
= ,其中u=lns,
,其中u=lns,
要使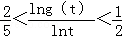 成立,只需
成立,只需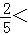
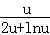
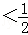 ,
,
即2<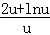
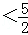 ,即2<2+
,即2<2+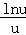
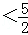 ,
,
只需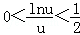 ,变形可得只需0<lnu<
,变形可得只需0<lnu<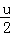 ,
,
当t>e2时,若s=g(t)≤e,则由f(s)的单调性,有t=f(s)≤f(e)=e2,矛盾,
所以s>e,即u>1,从而lnu>0成立,
另一方面,令F(u)=lnu﹣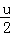 ,u>1,F′(u)=
,u>1,F′(u)=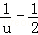 ,
,
令F′(u)=0,可解得u=2,
当1<u<2时,F′(u)>0,当u>2时,F′(u)<0,
故函数F(u)在u=2处取到极大值,也是最大值F(2)=ln2﹣1<0,
故有F(u)=lnu﹣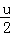 <0,即lnu<
<0,即lnu<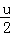 ,
,
综上可证:当t>e2时,有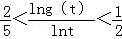 成立.
成立.
求导数可得f′(x)=2xlnx+x2•
 =2xlnx+x=x(2lnx+1),
=2xlnx+x=x(2lnx+1),令f′(x)=0,可解得x=
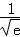 ,
,当x变化时,f′(x),f(x)的变化情况如下表:
| x | (0,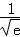 ) ) | 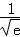 | ( 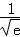 ,+∞) ,+∞) |
| f′(x) | ﹣ | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
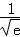 ),单调递增区间为(
),单调递增区间为( 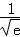 ,+∞)
,+∞)(2)证明:当0<x≤1时,f(x)≤0,设t>0,令h(x)=f(x)﹣t,x∈[1,+∞),
由(1)可知,h(x)在区间(1,+∞)单调递增,h(1)=﹣t<0,h(et)=e2tlnet﹣t=t(e2t﹣1)>0,
故存在唯一的s∈(1,+∞),使得t=f(s)成立;
(3)证明:因为s=g(t),由(2)知,t=f(s),且s>1,
从而
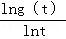 =
=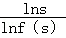 =
=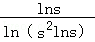 =
=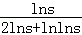 =
= ,其中u=lns,
,其中u=lns,要使
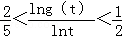 成立,只需
成立,只需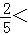
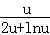
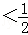 ,
,即2<
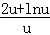
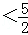 ,即2<2+
,即2<2+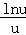
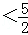 ,
,只需
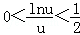 ,变形可得只需0<lnu<
,变形可得只需0<lnu<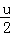 ,
,当t>e2时,若s=g(t)≤e,则由f(s)的单调性,有t=f(s)≤f(e)=e2,矛盾,
所以s>e,即u>1,从而lnu>0成立,
另一方面,令F(u)=lnu﹣
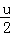 ,u>1,F′(u)=
,u>1,F′(u)=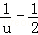 ,
,令F′(u)=0,可解得u=2,
当1<u<2时,F′(u)>0,当u>2时,F′(u)<0,
故函数F(u)在u=2处取到极大值,也是最大值F(2)=ln2﹣1<0,
故有F(u)=lnu﹣
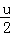 <0,即lnu<
<0,即lnu<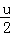 ,
,综上可证:当t>e2时,有
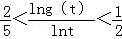 成立.
成立.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
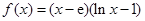
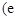 为自然对数的底数).
为自然对数的底数).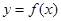 在
在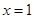 处的切线方程;
处的切线方程;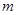 是
是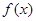 的一个极值点,且点
的一个极值点,且点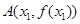 ,
,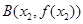 满足条件:
满足条件: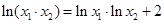 .
.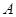 ,
,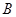 ,
,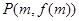 是三个不同的点,且构成直角三角形.
是三个不同的点,且构成直角三角形.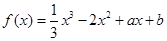 的图象在点
的图象在点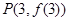 处的切线方程为
处的切线方程为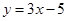 .
.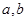 的值;
的值;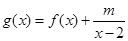 .
.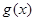 是
是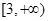 上的增函数,求实数
上的增函数,求实数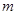 的最大值;
的最大值; ,使得过点
,使得过点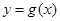 围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点
围成两个封闭图形,则这两个封闭图形的面积总相等.若存在,求出点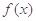 是
是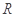 上的可导函数,
上的可导函数,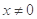 时,
时,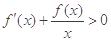 ,则函数
,则函数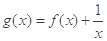 的零点个数为( )
的零点个数为( )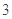

 .
.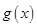 的单调区间;
的单调区间;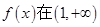 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;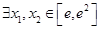 ,使
,使 成立,求实数a的取值范围.
成立,求实数a的取值范围.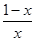 +ln x对任意x∈[
+ln x对任意x∈[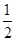 ,2]恒成立,则a的最大值为( )
,2]恒成立,则a的最大值为( )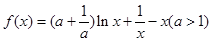 .
.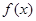 在
在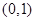 上的单调性;
上的单调性;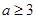 时,曲线
时,曲线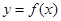 上总存在相异两点,
上总存在相异两点,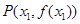 ,
,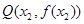 ,使得
,使得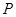 、
、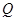 处的切线互相平行,求证:
处的切线互相平行,求证: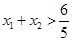 .
.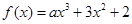 ,若
,若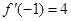 ,则
,则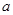 的值等于 ( )
的值等于 ( )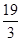
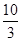
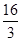
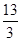
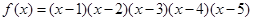 则
则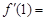 .
.