题目内容
7.已知直线$l:y=\sqrt{3}x+2$与圆O:x2+y2=4相交于A,B两点,则|AB|=$2\sqrt{3}$.分析 由圆的方程x2+y2=4,我们可以确定圆心的坐标及圆的半径,代入点到直线距离公式,即可求出弦心距,然后根据半弦长,弦心距,圆半径构成直角三角形,满足勾股定理,构造方程,解方程求出半弦长,进而即可得到答案.
解答 解:由已知可得圆x2+y2=4是以原点为圆心,以为半径的圆
则圆心到直线$l:y=\sqrt{3}x+2$距离d=$\frac{2}{\sqrt{3+1}}$=1
根据半弦长,弦心距,圆半径构成直角三角形,满足勾股定理得:$\frac{1}{2}$|AB|=$\sqrt{4-1}$=$\sqrt{3}$,
∴|AB|=$2\sqrt{3}$.
故答案为:$2\sqrt{3}$.
点评 本题考查的知识点是直线与圆相交的性质,其中半弦长,弦心距,圆半径构成直角三角形,满足勾股定理,是求圆的弦长时最常用的方法,一定要熟练掌握.

练习册系列答案
相关题目
18.已知函数y=sin(πx+φ)-2cos(πx+φ)(0<φ<π)的图象关于直线x=1对称,则sin2φ=( )
| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
15.已知l,m,n为两两垂直的三条异面直线,过l作平面α与m垂直,则n与α的关系是( )
| A. | n∥α | B. | n∥α或n?α | C. | n?α或n与α不平行 | D. | n?α |
2.下列命题中,真命题是( )
| A. | “?x∈R,x2≥x”的否定为“?x∉R,x2≥x” | |
| B. | 命题“若x=1,则x2=1”逆命题 | |
| C. | “若$\sqrt{3}x(x≠0)$是有理数,则x为无理数”的逆否命题 | |
| D. | “x<-1”是“x2-1>0”的必要不充分条件条件 |
12.(理)现有11个保送大学的名额分配给8个班级,每班至少有1个名额,则名额分配的方法共有( )
| A. | 56种 | B. | 112种 | C. | 120种 | D. | 240种 |
19.已知函数y=f(x)对任意自变量x都有f(x+1)=f(1-x),且函数f(x)在[1,+∞)上单调.若数列{an}是公差不为0的等差数列,且f(a6)=f(a20),则{an}的前25项之和为( )
| A. | 0 | B. | $\frac{25}{2}$ | C. | 25 | D. | 50 |
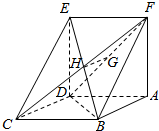 如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点,记CD=x,V(x)表示四棱锥F-ABCD的体积.
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD,G,H分别是DF,BE的中点,记CD=x,V(x)表示四棱锥F-ABCD的体积.