题目内容
(本题满分14分)设函数![]() (1)当
(1)当![]() 时,求
时,求![]() 的最大值;(2)令
的最大值;(2)令![]() ,(0
,(0![]() ≤3),其图象上任意一点
≤3),其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() ≤
≤![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围; (3)当
的取值范围; (3)当![]() ,
,![]() ,方程
,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值。
的值。
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() ≥
≥![]() (Ⅲ)
(Ⅲ)![]()
解析:
(1)依题意,知![]() 的定义域为(0,+∞)当
的定义域为(0,+∞)当![]() 时,
时,![]() ,
,
![]() (2′)
(2′)
令![]() =0,解得
=0,解得![]() .(∵
.(∵![]() )因为
)因为![]() 有唯一解,所以
有唯一解,所以![]()
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,此时
,此时![]() 单调递减。
单调递减。
所以![]() 的极大值为
的极大值为![]() ,此即为最大值。(5′)
,此即为最大值。(5′)
(2)![]() ,
,![]() ,则有
,则有![]() ≤
≤![]() ,在
,在![]() 上恒成立,
上恒成立,
所以![]() ≥
≥![]() ,
,![]() (8′)
(8′)
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,所以
,所以![]() ≥
≥![]() (10′)
(10′)
(3)因为方程![]() 有唯一实数解,所以
有唯一实数解,所以![]() 有唯一实数解,
有唯一实数解,
设![]() ,则
,则![]() . 令
. 令![]() ,得
,得![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() (舍去),
(舍去),![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在(0,
在(0,![]() )上单调递减,
)上单调递减,
当![]() 时,
时,![]() ,
,![]() 在(
在(![]() ,+∞)单调递增
,+∞)单调递增
当![]() 时,
时,![]() =0,
=0,![]() 取最小值
取最小值![]() .(12′)
.(12′)
则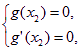 既
既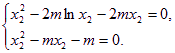
所以![]() ,因为
,因为![]() ,所以
,所以![]() (*)
(*)
设函数![]() ,因为当
,因为当![]() 时,
时,![]() 是增函数,所以
是增函数,所以![]() 至多有一解。
至多有一解。
因为![]() ,所以方程(*)的解为
,所以方程(*)的解为![]() ,即
,即![]() ,解得
,解得![]() .(14′)
.(14′)

练习册系列答案
相关题目
 的左、右焦点分别为F1与
的左、右焦点分别为F1与 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。 变成曲线
变成曲线 ,直线
,直线 与曲线
与曲线 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点) 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 满足
满足 ”
” 是集合M中的元素;
是集合M中的元素;
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。  .
. ,求函数
,求函数 的极值;
的极值; ,试确定
,试确定 的单调性;
的单调性; ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.