题目内容
【题目】如图,一块弓形余布料EMF,点M为弧![]() 的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=
的中点,其所在圆O的半径为4 dm(圆心O在弓形EMF内),∠EOF=![]() .将弓形余布料裁剪成尽可能大的矩形ABCD(不计损耗), AD∥EF,且点A、D在弧
.将弓形余布料裁剪成尽可能大的矩形ABCD(不计损耗), AD∥EF,且点A、D在弧![]() 上,设∠AOD=
上,设∠AOD=![]() .
.
(1)求矩形ABCD的面积S关于![]() 的函数关系式;
的函数关系式;
(2)当矩形ABCD的面积最大时,求cos![]() 的值.
的值.
【答案】(1) 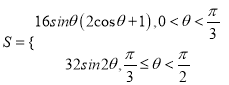 (2) cosθ=
(2) cosθ=![]()
【解析】试题分析: ![]() 分类讨论,求出
分类讨论,求出![]() ,可得矩形
,可得矩形![]() 的面积与关于
的面积与关于![]() 的函数解析式。
的函数解析式。
![]() 求导确定函数的单调性,即可求
求导确定函数的单调性,即可求![]() 的值。
的值。
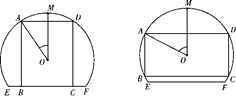
解析:(1) 设矩形铁片的面积为S,∠AOM=θ.
当0<θ<![]() 时(如图1),AB=4cosθ+2,AD=2×4sinθ,
时(如图1),AB=4cosθ+2,AD=2×4sinθ,
S=AB×AD= (4cosθ+2)(2×4sinθ)=16sinθ(2cosθ+1).
当![]() ≤θ<
≤θ<![]() 时(如图2),AB=2×4cos θ,AD=2×4sin θ,
时(如图2),AB=2×4cos θ,AD=2×4sin θ,
故S=AB×AD=64sinθcosθ=32sin 2θ.
综上得,矩形铁片的面积S关于θ的函数关系式为
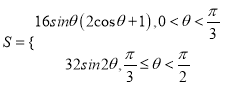
(2) 当0<θ<![]() 时,求导,得S′=16[cosθ(2cosθ+1)+sinθ(-2sinθ)]
时,求导,得S′=16[cosθ(2cosθ+1)+sinθ(-2sinθ)]
=16(4cos2 θ+cos θ-2).
令S′=0,得cosθ=![]() . 记区间
. 记区间![]() 内余弦值等于
内余弦值等于![]() 的角为θ0(唯一存在),
的角为θ0(唯一存在),
列表:
θ | (0,θ0) | θ0 |
|
S′ | + | 0 | - |
S | 极大值 |
又当![]() ≤θ<
≤θ<![]() 时,S=32sin2θ是单调减函数,所以当θ=θ0,即cosθ=
时,S=32sin2θ是单调减函数,所以当θ=θ0,即cosθ=![]() 时,矩形铁片的面积最大.
时,矩形铁片的面积最大.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目