题目内容
14.某校鲁班学习小组利用课余时间模拟制作奥运圣火采集器,已知他们制作采集器的抛物面的轴切线为经过定点P(1,2)的抛物线,则该抛物线的焦点与双曲线x24-y212=1在一三象限内的渐近线的距离为( )| A. | √32 | B. | 12或116 | C. | 116 | D. | √32或116 |
分析 求出抛物线的方程,可得焦点坐标,利用点到直线的距离公式,可得结论.
解答 解:由题设抛物线的标准方程为y2=2p1x或x2=2p2y,则22=2p1,∴p1=2,
从而焦点坐标为(1,0),
同理p2=14,从而焦点坐标为(0,18),
又双曲线x24-y212=1在一三象限内的渐近线的方程为y-√3x=0,
∴该抛物线的焦点与双曲线x24-y212=1在一三象限内的渐近线的距离为|(−√3)×1+0×1|√3+1=√32
或|(−√3)×0+18×1|√3+1=116,
故选:D.
点评 本题考查抛物线、双曲线的性质,考查点到直线的距离公式,考查学生的计算能力,属于中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧
如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧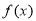 为奇函数,且当
为奇函数,且当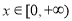 时,
时,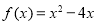 ,则
,则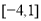 上的最大值为( )
上的最大值为( )