题目内容
当 时,函数
时,函数 的单调性
的单调性
| A.是单调增函数 |
| B.是单调减函数 |
C.在 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
D.在 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C
解析试题分析: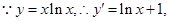 令
令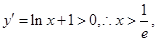 所以当
所以当 时,函数
时,函数 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
考点:本小题主要考查函数的单调性的判断.
点评:导数是判断单调性的有力工具,导数在某个区间上大于零,则函数单调递增,在某个区间上小于零,则函数单调递减,不要忘记函数的定义域.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
下列函数在其定义域内,既是奇函数又存在零点的是( )
A. | B. |
C. | D.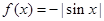 |
函数 在区间
在区间 上( )
上( )
| A.没有零点 | B.只有一个零点 | C.有两个零点 | D.以上选项都错误 |
函数 定义如下:对任意
定义如下:对任意 ,当
,当 为有理数时,
为有理数时, ;当
;当 为无理数时,
为无理数时, ;则称函数
;则称函数 为定义在实数上的狄利克雷拓展函数.下列关于函数
为定义在实数上的狄利克雷拓展函数.下列关于函数 说法错误的是( )
说法错误的是( )
A. 的值域为 的值域为 |
B. 是偶函数 是偶函数 |
C. 是周期函数且 是周期函数且 是 是 的一个周期 的一个周期 |
D. 在实数集上的任何区间都不是单调函数 在实数集上的任何区间都不是单调函数 |
设点 在曲线
在曲线 上,点
上,点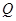 在曲线
在曲线 上,则
上,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
函数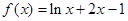 的零点所在区间为
的零点所在区间为
A.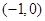 | B.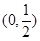 | C.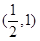 | D. |
已知 为定义在
为定义在 上的可导函数,且
上的可导函数,且
 对于任意
对于任意 恒成立,则( )
恒成立,则( )
A. , , |
B. , , |
C. , , |
D. , , |
若 ,则
,则 的大小关系
的大小关系
A. | B. |
C. | D. |
 对于区间D内任意的
对于区间D内任意的 ,有
,有

 成立,称
成立,称 在区间
在区间 上是 “凸函数”,则在△
上是 “凸函数”,则在△ 中,
中, 的最大值是( )
的最大值是( )


