题目内容
函数 在区间
在区间 上( )
上( )
| A.没有零点 | B.只有一个零点 | C.有两个零点 | D.以上选项都错误 |
B
解析试题分析:因为函数 的对称轴为x=2,又
的对称轴为x=2,又 ,所以函数
,所以函数 在区间
在区间 上只有一个零点。
上只有一个零点。
考点:函数的零点。
点评:我们要充分理解函数零点存在性定理。满足函数零点存在性定理的条件,则一定存在零点;但存在零点,不一定满足函数零点存在性定理。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知方程 在
在 有两个不同的解
有两个不同的解 (
( ),则下面结论正确的是:
),则下面结论正确的是:
A. | B. |
C. | D. |
函数 的零点个数是
的零点个数是
| A.0 | B.1 |
| C.2 | D.3 |
已知定义在R上的函数f(x)满足f(x+1)=-f(x)。当x [0,1]时,f(x)=
[0,1]时,f(x)= -x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
-x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
A.(- , , ) ) | B.(- , , ] ] | C. | D.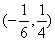 |
当 时,函数
时,函数 的单调性
的单调性
| A.是单调增函数 |
| B.是单调减函数 |
C.在 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
D.在 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
函数 的定义域是( )
的定义域是( )
A. | B. | C.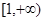 | D. |
函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. | C. | D. |
 是定义在
是定义在 上的偶函数,且对任意的
上的偶函数,且对任意的
 .当
.当 时,
时, .若直线
.若直线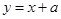 与函数
与函数 的图象有两个不同的公共点,则实数
的图象有两个不同的公共点,则实数 的值为( )
的值为( )



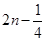
 的图象如左图,那么导函数
的图象如左图,那么导函数 的图象可能是( )
的图象可能是( )
