题目内容
如果函数 对于区间D内任意的
对于区间D内任意的 ,有
,有

 成立,称
成立,称 是区间D上的“凸函数”.已知函数
是区间D上的“凸函数”.已知函数 在区间
在区间 上是 “凸函数”,则在△
上是 “凸函数”,则在△ 中,
中, 的最大值是( )
的最大值是( )
A. | B. | C. | D. |
D
解析试题分析:利用“凸函数”的定义得到恒成立的不等式,利用三角形的内角和为π,求出函数的最大值.解:∵y=sinx在区间[0,π]上是“凸函数”,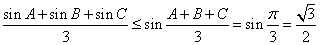 可知
可知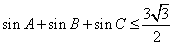 ,故选D.
,故选D.
考点:新定义的运用
点评:本题考查理解题中的新定义、并利用新定义求最值、考查三角形的内角和为π.

练习册系列答案
相关题目
若函数 ,则对于不同的实数a,函数
,则对于不同的实数a,函数 的单调区间个数不可能是( )
的单调区间个数不可能是( )
| A.1个 | B.2个 | C.3个 | D.5个 |
设f(x)是定义在R上的偶函数,对x∈R,都有f(x+4)=f(x),且当x∈[-2,0]时,f(x)=( )x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是
| A.(1,2) | B.(2,+∞) | C.(1, ) ) | D.( ,2) ,2) |
已知方程 在
在 有两个不同的解
有两个不同的解 (
( ),则下面结论正确的是:
),则下面结论正确的是:
A. | B. |
C. | D. |
函数 的零点个数是
的零点个数是
| A.0 | B.1 |
| C.2 | D.3 |
当 时,函数
时,函数 的单调性
的单调性
| A.是单调增函数 |
| B.是单调减函数 |
C.在 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
D.在 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
在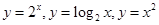 ,这三个函数中,当
,这三个函数中,当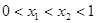 时,
时,
使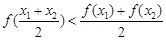 恒成立的函数的个数是( )
恒成立的函数的个数是( )
A. 个 个 | B. 个 个 | C.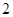 个 个 | D.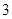 个 个 |
 表示大于
表示大于 的最小整数,例如
的最小整数,例如 .下列命题
.下列命题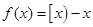 的值域是
的值域是 ;②若
;②若 是等差数列,则
是等差数列,则 也是等差数列;
也是等差数列; ,则方程
,则方程 有3个根.
有3个根. 的图象如左图,那么导函数
的图象如左图,那么导函数 的图象可能是( )
的图象可能是( )
