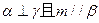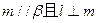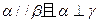题目内容
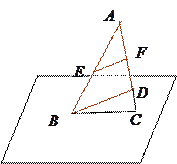
(12分)如图,在四面体ABCD中,CB="CD," AD⊥BD,点E、F分别是AB, BD的中点,求证:
(1)直线EF//平面ACD;
(2)平面EFC⊥平面BCD。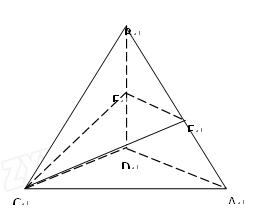
(1)直线EF//平面ACD;
(2)平面EFC⊥平面BCD。

略
证明:(1)∵EF是ΔBAD的中位线,∴EF//AD,又EF?平面ACD,AD?平面ACD,
∴EF//平面 ACD。
(2)∵EF//AD, AD⊥BD, ∴BD⊥EF, 又∵BD⊥CF,
∴BD⊥平面BCD,又BD?平面EFC,∴平面 EFC⊥平面 BCD。
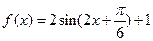
∴EF//平面 ACD。
(2)∵EF//AD, AD⊥BD, ∴BD⊥EF, 又∵BD⊥CF,
∴BD⊥平面BCD,又BD?平面EFC,∴平面 EFC⊥平面 BCD。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
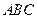 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为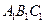 ,
,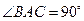 ,
,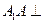 平面
平面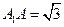 ,
,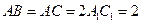 ,
,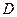 为
为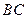 中点.
中点.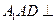 平面
平面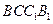 ;
;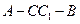 的大小.
的大小.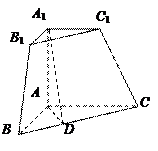
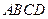 中,
中,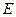 ,
,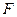 分别是
分别是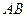 ,
,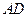 的中点.
的中点.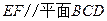 .
.
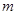 、
、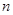 与平面
与平面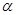 、
、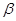 ,下列命题正确的是 ( )
,下列命题正确的是 ( )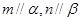 且
且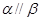 ,则
,则
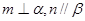 且
且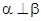 ,则
,则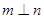
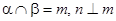 且
且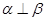 ,则
,则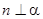
 且
且
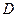 为
为 的中点,
的中点,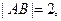
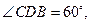
 为
为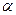 内的动点,且
内的动点,且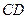 的距离为
的距离为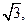 则
则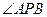 的最大值为( )
的最大值为( )
 0°
0°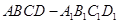 ,长为2的线段
,长为2的线段 的一个端点
的一个端点 在
在 上
上 在底面
在底面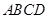 上运动.则线段
上运动.则线段 的轨迹与正方体的表面所
的轨迹与正方体的表面所



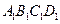 中E是AB的中点,O是侧面
中E是AB的中点,O是侧面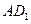 的中心.
的中心.








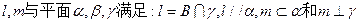 ,那么必有( )
,那么必有( )