题目内容
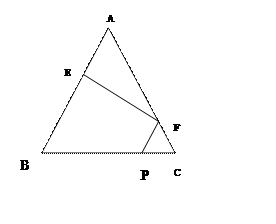
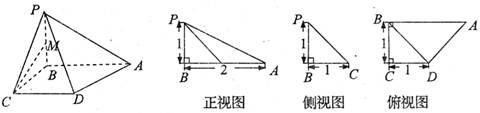
(本题满分14分)在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足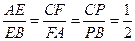 ,将
,将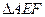 沿EF折起到
沿EF折起到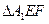 的位置,使二面角
的位置,使二面角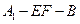 成直二面角,连结
成直二面角,连结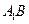 ,
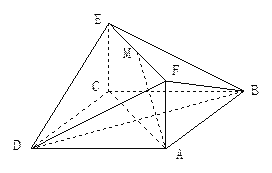
,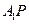 (如图)(I)求证:
(如图)(I)求证: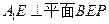 (Ⅱ)求点B到面
(Ⅱ)求点B到面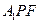 的距离(Ⅲ)求异面直线BP与
的距离(Ⅲ)求异面直线BP与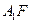 所成角的余弦
所成角的余弦

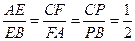 ,将
,将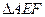 沿EF折起到
沿EF折起到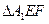 的位置,使二面角
的位置,使二面角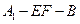 成直二面角,连结
成直二面角,连结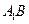 ,
,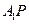 (如图)(I)求证:
(如图)(I)求证: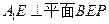 (Ⅱ)求点B到面
(Ⅱ)求点B到面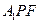 的距离(Ⅲ)求异面直线BP与
的距离(Ⅲ)求异面直线BP与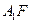 所成角的余弦
所成角的余弦

(Ⅰ)见解析 (Ⅱ) 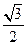 (Ⅲ)
(Ⅲ)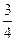
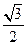 (Ⅲ)
(Ⅲ)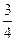
(I)在图1中,取BE的中点D,连DF
∵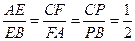 ,∵
,∵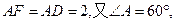 ∴
∴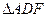 为正三角形
为正三角形
又∵AE="ED=1 " ∴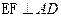 ∴在图2中有
∴在图2中有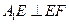 ,
,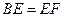
∴ 为二面角
为二面角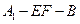 的平面角
的平面角
∵二面角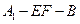 为直二面角 ∴
为直二面角 ∴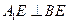
又∵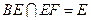 ∴
∴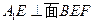 即
即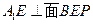 …………5分
…………5分
(Ⅱ)∵BE//PF ∴BE//面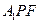 ∵B到面
∵B到面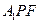 的距离即为E到面
的距离即为E到面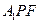 的距离,
的距离,
∵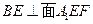 ,又BE//PF,∴
,又BE//PF,∴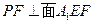
∴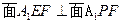 ∵E到面
∵E到面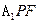 的距离即为
的距离即为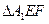 中E到
中E到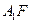 的距离
的距离
d=A1E×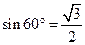 ∴点B到面
∴点B到面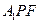 的距离为
的距离为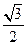 ………………10分
………………10分
(Ⅲ)∵DF//BP ∴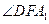 即为所求角
即为所求角
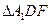 中
中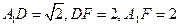 ,
,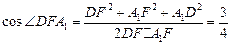
∴异面直线BP与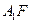 所成角的余弦值为
所成角的余弦值为 ………………14分
………………14分
法二:(建立空间直角坐标系,略解)
∵
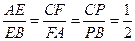 ,∵
,∵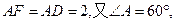 ∴
∴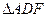 为正三角形
为正三角形又∵AE="ED=1 " ∴
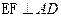 ∴在图2中有
∴在图2中有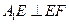 ,
,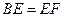
∴
 为二面角
为二面角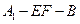 的平面角
的平面角∵二面角
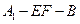 为直二面角 ∴
为直二面角 ∴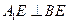
又∵
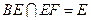 ∴
∴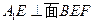 即
即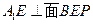 …………5分
…………5分(Ⅱ)∵BE//PF ∴BE//面
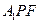 ∵B到面
∵B到面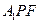 的距离即为E到面
的距离即为E到面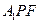 的距离,
的距离,∵
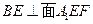 ,又BE//PF,∴
,又BE//PF,∴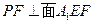
∴
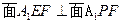 ∵E到面
∵E到面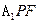 的距离即为
的距离即为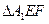 中E到
中E到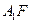 的距离
的距离d=A1E×
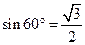 ∴点B到面
∴点B到面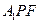 的距离为
的距离为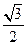 ………………10分
………………10分(Ⅲ)∵DF//BP ∴
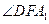 即为所求角
即为所求角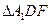 中
中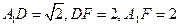 ,
,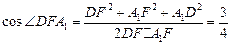
∴异面直线BP与
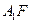 所成角的余弦值为
所成角的余弦值为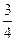 ………………14分
………………14分法二:(建立空间直角坐标系,略解)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
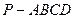 中,底面
中,底面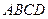 是直角梯形,
是直角梯形,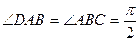 ,且
,且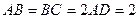 ,侧面
,侧面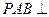 底面
底面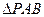 是等边三角形.
是等边三角形.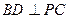 ;
;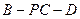 的大小.
的大小.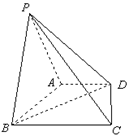
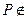 面ABCD,过BC作平面BCFE交AP于E,
面ABCD,过BC作平面BCFE交AP于E,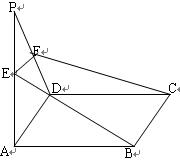
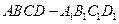 中,
中,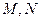 分别是
分别是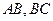 中点.
中点.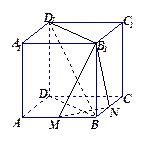
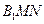 ⊥平面
⊥平面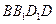 ;
;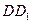 上有一点
上有一点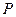 ,使
,使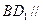 平面
平面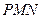 ,求
,求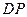 与
与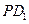 的比.
的比.
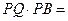
 和矩形
和矩形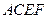 所在的平面互相垂直,
所在的平面互相垂直,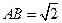 ,
,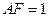 ,
,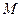 是线段
是线段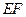 的中点.
的中点.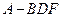 的体积;
的体积;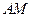 //平面
//平面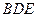 ;
;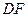 所成的角.
所成的角.