题目内容
【题目】已知函数f(x)= ![]() 图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,则实数k的取值范围为( )
A.(1,2)
B.(﹣1,0)
C.(﹣2,﹣1)
D.(﹣6,﹣1)
【答案】C
【解析】解:∵函数f(x)= ![]() 图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,
图象上有且仅有四个不同的点关于直线y=e的对称点在函数g(x)=kx+2e+1的图象上,
而函数g(x)=kx+2e+1关于直线y=e的对称图象为y=﹣kx﹣1,
∴函数ff(x)= ![]() 图象与y=﹣kx﹣1的图象有且只有四个不同的交点,
图象与y=﹣kx﹣1的图象有且只有四个不同的交点,
作函数f(x)= ![]() 图象与y=﹣kx﹣1的图象如下,
图象与y=﹣kx﹣1的图象如下,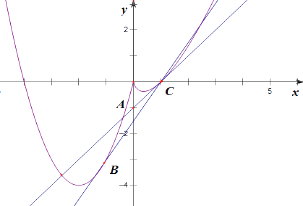 ,
,
易知直线y=﹣kx﹣1恒过点A(0,﹣1),
设直线AC与y=xlnx相切于点C(x,xlnx),
y′=lnx+1,
故lnx+1= ![]() ,
,
解得,x=1;
故kAC=1;
设直线AB与y=xlnx相切于点C(x,x2+4x),
y′=2x+4,
故2x+4= ![]() ,
,
解得,x=﹣1;
故kAC=﹣2+4=2;
故1<﹣k<2,
故﹣2<k<﹣1;
故选:C.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
【题目】随着互联网的发展,移动支付![]() 又称手机支付
又称手机支付![]() 逐渐深入人民群众的生活
逐渐深入人民群众的生活![]() 某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对
某学校兴趣小组为了了解移动支付在人民群众中的熟知度,对![]() 岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表
岁的人群随机抽样调查,调查的问题是你会使用移动支付吗?”其中,回答“会”的共有50个人,把这50个人按照年龄分成5组,并绘制出频率分布表![]() 部分数据模糊不清
部分数据模糊不清![]() 如表:
如表:
分组 | 频数 | 频率 | |
第1组 |
| 10 |
|
第2组 |
|
|
|
第3组 |
| 15 |
|
第4组 |
|
|
|
第5组 |
| 2 |
|
合计 | 50 |
| |
![]() 表中
表中![]() 处的数据分别是多少?
处的数据分别是多少?
![]() 从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
从第1组,第3组,第4组中用分层抽样的方法抽取6人,求每组抽取的人数.
![]() 在
在![]() 抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.