Question

【题目】已知函数f（x）是定义域为R的奇函数，其中m是常数．

（Ⅰ）判断f（x）的单调性，并用定义证明；

（Ⅱ）若对任意x∈[﹣3，1]，有f（tx）+f（2t﹣1）≤0恒成立，求实数t的取值范围．

Answer 1

【答案】（Ⅰ）增函数，见解析（Ⅱ）．

【解析】

（Ⅰ）根据函数为奇函数得到m＝1，再设x1＜x2，再计算得到证明.

（Ⅱ）利用函数奇偶性变换得到f（tx）≤f（1﹣2t）得到（x+2）t≤1，得到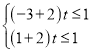

计算得到答案.

（Ⅰ）f（x）是R上的增函数，证明如下：

由f（x）是奇函数，所以f（x）+f（﹣x）＝0，

∴，化为∴m＝1，

∴f（x）＝ex﹣e﹣x，

设x1＜x2，则，

由于y＝ex是增函数，所以，

∴f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），

∴函数f（x）是R上的增函数；

（Ⅱ）由于f（x）是R上的奇函数，所以由f（tx）+f（2t﹣1）≤0恒成立

可得f（tx）≤﹣f（2t﹣1）＝f（1﹣2t），

∴tx≤1﹣2t，（x+2）t≤1，

当x∈[﹣3，1]时，上式恒成立，则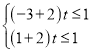，解得，

∴实数t的取值范围为